In the section on Prisms, we discussed a "stacking technique" used to demonstrate the formula for volume. Seventeenth century mathematician, Bonaventura Cavalieri, utilized this stacking concept in comparing the areas and volumes of various shapes.
Cavalieri's Principle in 2D: |
|
This first section deals with Cavalieri's ideas in relation to comparing the areas of figures.
Cavalieri's Priniciple in 2D: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. |
|
When we developed the formula for the area of a parallelogram, we dissected the parallelogram and re-assembled it to form a rectangle of equal base and height.
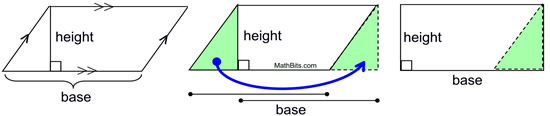
This idea of disassembling figures to compare their areas can also be accomplished using cross sectional stacking. It was an interest in this stacking concept that led to Cavalieri's Principles.
We know that the formula for the area of a rectangle is "base" times "height". The rectangle at the right has been sliced into 8 congruent sections. The sections have then been pushed to the right to form a slanted figure. |
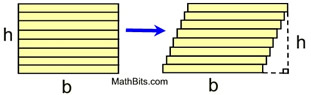 |
The slanted figure has the same base, height and area as the rectangle, yet it is not a rectangle. The slanted figure resembles a parallelogram (except for all of the jagged edges). As we saw with the stacking technique, if we had sliced hundreds of very, very very thin sections, instead of 8 thick sections, we would see the parallelogram more clearly. The parallelogram will have the same area as the original rectangle.
Cavalieri described this relationship between figures using parallel lines.
Since parallel lines are everywhere equidistant, his figures ("regions") are of equal height.
Conditions:
•
2 parallel lines (p || q)
• two figures between the parallel lines
• every additional line parallel to p and q,
must cut equal widths on both figures
Conclusion:
• the areas of the two figures are equal |
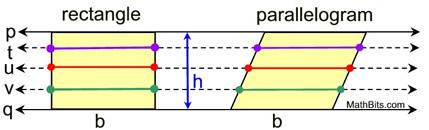 |
In plain English, Cavalieri stated "if two figures have the same height, and "matching" congruent widths everywhere along the height, the figures have the same area." Note that the "congruent widths" need not be of the same lengths on each of the parallel lines.
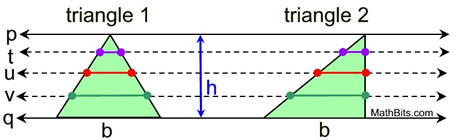
The area of triangle 1 = the area of triangle 2.
 The converse of Cavalieri's Principle in 2D is not true! The converse of Cavalieri's Principle in 2D is not true!
Given two figures with the same height and the same area, it is not necessarily true that parallel slices along the height always produce matching congruent widths.
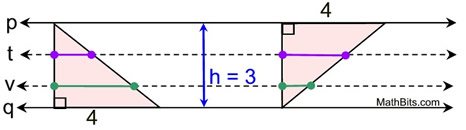 These two triangle have the same base, height and area.
These two triangle have the same base, height and area.
But, the matching widths on the parallel lines are NOT congruent.
Yes, they COULD be re-arranged to satisfy Cavalieri's principle,
but as they appear above,
Cavalieri's principle does not apply. |

Cavalieri's Principle in 3D: |
|
This section deals with Cavalieri's ideas in relation to comparing the volumes of solids.
Cavalieri's Priniciple in 3D: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes. |
|
The formula for the volume of a prism is the "area of the base" times the "height". The right triangular prism shown has been sliced into 15 congruent sections parallel to the bases. The sections have then been slid to the right to form a slanted solid. Notice the jagged edges of the slanted solid.
|
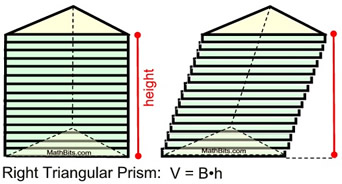 |
Since the right triangular prism and the slanted solid are composed of the same cut up sections, they have the same volumes.
If we increase the number of slices so the thickness of the sections becomes extremely, extremely small, the slices can be referred to as "cross sections" and the slanted solid can be seen as an oblique prism. The right triangular prism and the oblique triangular prism will have the same volume.
Cavalieri extended his 2-D principle to 3-D and introduced parallel planes and areas to describe the relationship between solids. Since the planes are parallel, the solids are of equal height.
Conditions:
•
2 parallel planes (p || q)
• two solids between the parallel planes
• every additional plane parallel to p and q,
must cut equal areas on both figures
Conclusion:
• the volumes of the two solids are equal |
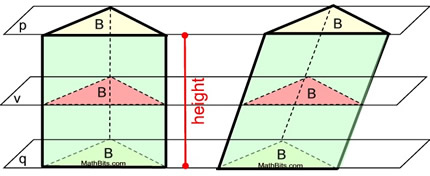 |
This right triangular prism and oblique triangular prism meet the conditions needed to apply Cavalieri's principle. They are the same height and the areas of the matching cross sections are equal. The volumes of these solids are equal.
In plain English, Cavalieri stated "if two solids have the same height, and "matching" equal areas everywhere along the height, the solids have the same volume."
NOTE: Cavalieri's principle also applies when comparing solids with differing base shapes. In the diagram at the right, if the areas of the triangular slices and the rectangular slices are equal when matched on parallel planes, the solids have equal volumes. |
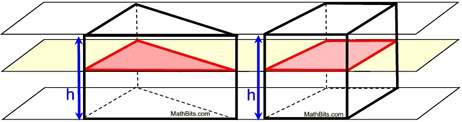
Right Triangular Prism Right Rectangular Prism |
Examples:
1. The triangular prism and the rectangular prism, shown at the right, have been sliced by a plane parallel to their bases creating the shaded cross sections.
a. Find the areas of the two cross sections.
b. Find the volumes of the two figures.
c. Does this demonstrate Cavalieri's Principle?
|
 |
a. Area of cross section for the triangular prism: ½•2•10 = 10
Area of cross section for the rectangular prism: 5•2 = 10
Areas of cross sections are the same.
b. Volume of the triangular prism: V = Bh = ½•2•10•6 = 60
Volume of the rectangular prism: V = Bh = 10•6 = 60
Volumes of the figures are the same.
c. This problem demonstrates Cavalieri's Principle in that these two figures are between two parallel planes 6 inches apart, and the areas of parallel cross sections of the two solids are equal. Thus, the volumes of the solids are equal.
|
2. Two cylinders each have a height of 6 inches. If the radius of cylinder A, x, equals the radius of cylinder B, y, then the volume of cylinder A is _____ the volume of cylinder B.
Which choice correctly fills the blank?
a) less than
b) greater than
c) equal to |
 |
The correct choice is "c".
The cylinders are between two parallel planes 6 inches apart.
Since a parallel cross section of the cylinders will be two circles of equal radii, the areas of these circular cross sections will be equal. If the areas of the cross sections are equal, then the volumes of the cylinders will be the same by Cavalieri's Principle.
|
Conclusion:
One of the benefits of Cavalieri's principle is that it allows us to determine the volume of an oblique prism (or oblique cylinder). When dealing with two prisms (or two cylinders), if the base areas are equal and the heights are equal, then the volume is V = Bh regardless of the overall shape. (When working with a cylinder, the base is a circle, so B = πr2.)
In a similar manner, it can be shown that volume formulas for pyramids and cones will also apply to both right and oblique solids, even though the matching parallel cross sections are not of equal areas along the height. As long as the "matching" cross section areas are equal, Cavalieri's principle applies.
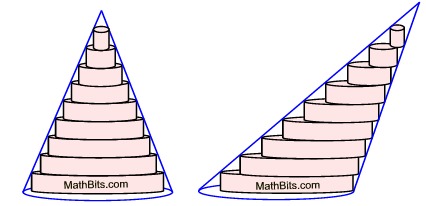
If these rather chunky slices were replaced with extremely thin slices (cross sections) parallel to the bases, and the matching areas
were equal, the volumes of this right circular cone and the oblique circular cone would be equal.











