|
|
A prism is a three-dimensional solid figure with two parallel faces, called bases, that are congruent polygons, and lateral flat faces which are rectangles in a right prism, and are parallelograms in an oblique prism.
|
|
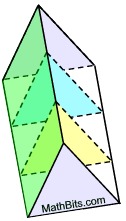
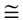 Cross Sections Cross Sections
(parallel to bases) |
• |
A prism is a polyhedron since its faces are polygons. |
• |
The bases are parallel and congruent. |
• |
The lateral faces are parallelograms. |
• |
The lateral edges are parallel and congruent. |
• |
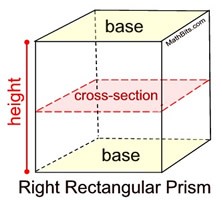
All cross sections of a prism parallel to the bases will be congruent to the bases. |
• |
Prisms are named for the shape of the bases. |
• |
Prisms do NOT always sit on their bases
(as shown in both the left and right diagrams). |
|
 Right Triangular Prism
Right Triangular Prism |
The following diagrams show various prisms with their bases shaded.
 Right Pentagonal Prism
Right Pentagonal Prism |
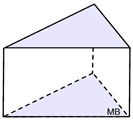 Right Triangular Prism
Right Triangular Prism |
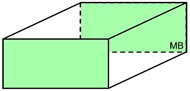 Right Rectangular Prism
Right Rectangular Prism |
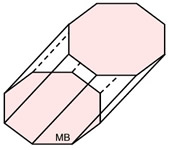 Oblique Octagonal Prism
Oblique Octagonal Prism |
Right vs Oblique Prisms:
In a right prism, the congruent (translated) bases will appear directly above one another when the prism is sitting on its base. The line segments joining the corresponding endpoints of each base are congruent, are parallel to one another, and are perpendicular to the bases. These parallel segments are referred to as lateral edges, and represent the height of the prism. The lateral faces in a right prism are rectangles.
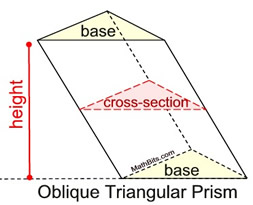
An oblique prism is one that seems to tilt at an angle. In an oblique prism, the congruent bases will NOT appear directly above one another when the prism is sitting on its base. The line segments joining the corresponding endpoints of each base are still congruent and are still parallel to one another, but are NOT perpendicular to the bases and do NOT represent the height of the prism. The height of an oblique prism does not lie on, nor is it parallel to, a lateral edge. The lateral faces in an oblique prism are parallelograms.
Cross sections parallel to the bases in each prism (right or oblique) will be congruent to the bases.
The "height" of a prism is the distance between the two bases. In a right prism, the height is a lateral edge.
In the case of the oblique prism, the height is the shortest line segment between the extended bases, as shown.

Volume of a Prism (for both right and oblique prisms):
The volume of a prism is its base area times its height. Vprism = Bh |
|
V = volume in cubic units; B = area of the base in square units; h = height in units
Examples: Volumes of Prisms
For a right rectangular prism:
You probably remember that the volume formula of a 3D "box" is V = l • w • h.

But, we now know that the formula can be expressed as V = B • h,
where B = the area of the base.
B = l • w so V = B • h |
For a right triangular prism:
Since the base is always a triangle, we know that the area of the base will be
B = ½ • b • h.

The volume will be V = B • h,
or in this case, V = B • l.
* Be careful no to confuse the "height" used in the triangular base ( h ) with the "height" of the triangular prism ( I ). |
Justification of Prism Volume Formula:
(For this discussion, our prism will be a right rectangular prism.)
As we proceed, keep in mind that if we "slice" a prism, parallel to its base, we will get the same congruent cross section no matter where the slice occurs. |
 |
The definition of "volume" is often stated as the amount of 3-dimensional space an object occupies. Since we measure volume in cubic units (a cube 1 unit by 1 unit by 1 unit), we can also refer to volume as the number of cubic units that will exactly fill the object.
|
 |
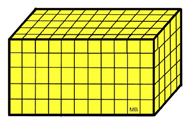 |
As you have done in the past, we will fill our prism with unit cubes. For ease of demonstration, our prism has integer dimensions so we will not have to worry about fractional parts of the cubes. Our prism contains 275 unit cubes (11 cubes by 5 cubes by 5 cubes) for a volume of 275 cubic units. |
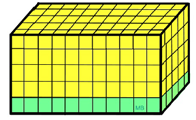
If we look at just the bottom layer of cubes, (a "portion" of the prism) we can model the volume by simply "stacking up" the bottom layer (the 55 cubes) times the 5 needed layers. This "stacking" technique assumes that each layer is exactly the same. |
|
| Notice that the bottom layer of 55 cubes is also the number of "square units" needed to cover the base (or the area of the base). Now, area is a two-dimensional concept and has no height (thickness), so we cannot "stack" it. But we can stack figures whose thickness is extremely small, and the smaller the thickness, the more accurate the volume. The thickness can be made so small that it has little effect on the calculations. This concept of obtaining increased accuracy as this thickness is made smaller and smaller and smaller is referred to as a "limiting" argument, which will be further discussed in PreCalculus and Calculus. |
We know that cross sections are two-dimensional figures that have no thickness. So how can they be stacked to "fill up" a prism? In reality, a two-dimensional figure cannot fill a prism. But theoretically, if the thickness is so very, very, very small that it has little effect on calculations (thickness getting close to zero), the stacking figure may be referred to as a "cross section", even though it is really a three-dimensional figure with very, very, very small thickness.
|
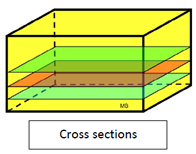 |
So, the volume of a prism can be found by multiplying the area of a very, very, very thin cross section (congruent to the bases and parallel to the bases) by the height of the prism. Generally speaking, the volume of a prism is found by multiplying the area of the base, B, by the height of the prism, h. Vprism = B • h |

Surface Area of a Prism:
The surface area of a prism is the sum of the areas of the bases plus the areas of the lateral faces. (The sum of the areas of all the faces.) |
|
Right Triangular Prism
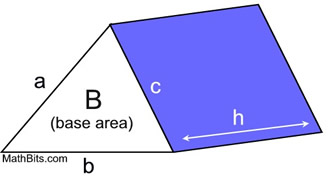
Surface Area, S, of a right prism:
S = 2B + ah + bh + ch
or
S = 2B + ph
B = area of prism's base
p = perimeter of prism's base (a + b + c)
h = height of the right prism |
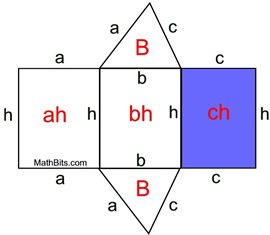
A net of this prism shows the "surfaces" whose areas, when added, comprise the surface area.
The red expressions represent areas of the sections.
In this example, B = area of the prism's base
= ½ (triangle's base) • (triangle's height). |

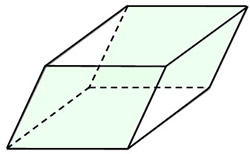
Parallelepiped
A prism which has a parallelogram as its base is called a parallelepiped. It is a polyhedron with 6 faces which are all parallelograms. |
|
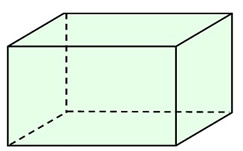
Cuboid
A cuboid is a closed box of three pairs of rectangular faces placed opposite one another and joined at right angles. It is a rectangular parallelepiped, rectangular prism, or a rectangular solid ("a box").
Its volume is V = l
• w• h.
Its surface area is SA = 2wl + 2lh + 2hw. |
|

See applications of prisms under Modeling. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|