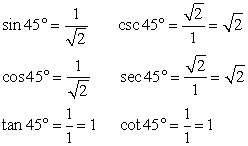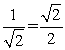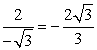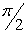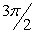|
The section Standard Position and Reference Angles showed how to determine reference "angles".
Those reference angles will now be put to use to form reference "triangles"
that will assist in dealing with trigonometric situations.
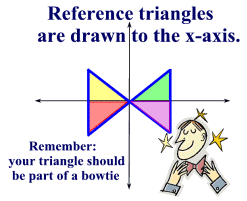
A reference triangle is formed by "dropping" a perpendicular from the terminal ray of a standard position angle to the x-axis. Remember, it must be drawn to the x-axis.
Reference triangles are used to find trigonometric values for their standard position angles. They are of particular importance for standard position angles whose terminal sides reside in quadrants II, III and IV. Remember that a reference triangle will contain the reference angle. |
|

Reference Triangles in the First Quadrant:
To form the reference triangle, simply drop a perpendicular from the terminal ray of the angle to the x-axis, forming a right triangle. In the first quadrant, the standard position angle is its own reference angle and is contained in the reference triangle.
|
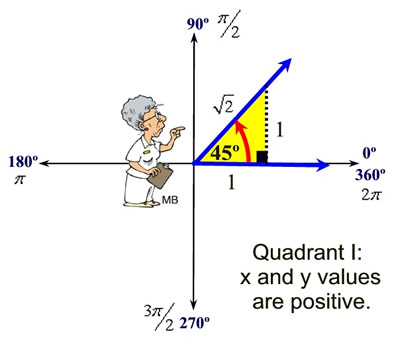 |
Since the standard position angle in this example is 45º, label the triangle with the values for the 45º-45º-90º patterns
You are now ready to find all six trigonometric functions. Notice that x and y values are positive in quadrant I.
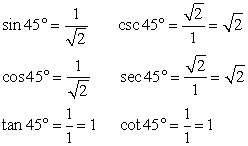 |

Reference Triangles in Quadrants II, III and IV:
When the terminal ray moves our angle into quadrants II, III, or IV, finding the trigonometric values becomes more of a challenge. When our angle moves out of the first quadrant, we must be aware of the sign of our function value.
|
 |
The reference angle and the reference triangle are used to find the trigonometric function values of angles in Quadrants II, III and IV.
Remember that the reference triangle contains the reference angle.
We will now start marking the ± signs on the legs of the right triangle. The hypotenuse is a directed segment and is considered positive.
(Yes, we know that the sides of a triangle are always positive in length. But we must be careful now to remember quadrant "direction".)
|
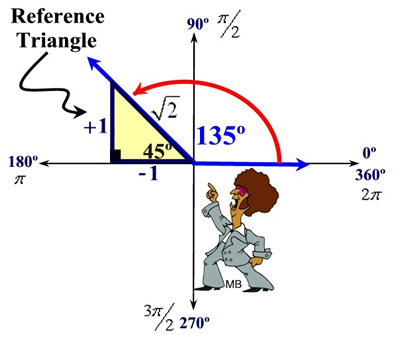
Example 1:
Find the exact value of sin 135º. (see diagram above)
Solution: Draw the angle in standard position (with initial ray on the x-axis and opening counterclockwise). Find the reference angle (in this case 45º). Draw the reference triangle. Label the sides of the triangle with the patterns for a 45º- 45º- 90º triangle, being careful to include the appropriate signs. Now read your answer of sine from the triangle.
Answer: 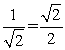 |
|
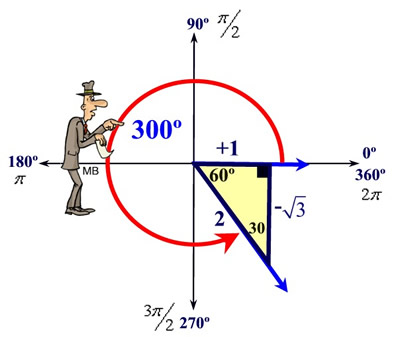
Example 2:
Find the exact value of csc 300º.
Solution: Draw the angle in standard position (with initial ray on the x-axis and opening counterclockwise). Find the reference angle (in this case 60º). Draw the reference triangle. Label the sides of the triangle with the patterns for a 30º- 60º- 90º triangle, being careful to include the appropriate signs. Now read your answer of cosecant from the triangle (hypotenuse over opposite side).
Answer: 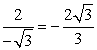 |
|

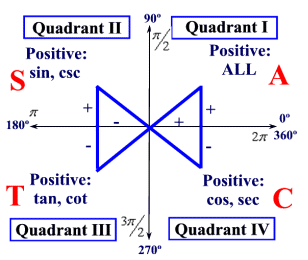
Chart for signs of Trigonometric Function Values:
|
Memorizing the chart at the right is not necessary as you can make these determinations by examining each quadrant.
If, however, you wish to remember such a chart, a mnemonic statement may be helpful for remembering the positive trig values (and their reciprocals) in each quadrant.
A S T C - All Students Take Calculus!
A S T C - All Silly Trig Classes! |
|

Quadrantal Angles:
A quadrantal angle has its terminal side coinciding with a coordinate axis. The trigonometric function value of such an angle can be determined by the coordinates of the point where the unit circle intersects the axis.
| θ |
Coordinate |
sin θ |
csc θ |
cos θ |
sec θ |
tan θ |
cot θ |
| 0, 0º, 2π |
(1,0) |
0 |
undefined |
1 |
1 |
0 |
undefined |
90º, 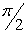 |
(0,1) |
1 |
1 |
0 |
undefined |
undefined |
0 |
| 180º, π |
(-1,0) |
0 |
undefined |
-1 |
-1 |
0 |
undefined |
270º, 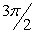 |
(0,-1) |
-1 |
-1 |
0 |
undefined |
undefined |
0 |
(Again, there is no need to memorize such a chart. Simply look at the point of interest and remember that sine is vertical length and cosine is horizontal length in a unit circle. The chart is displayed here to show the combination of answers.)
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|