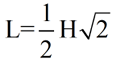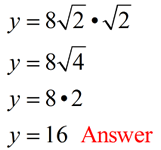|

There are two "special" right triangles that will continually appear throughout your study of mathematics: the 30º-60º-90º triangle and the 45º-45º-90º triangle. The special nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions. This page will deal with the 45º-45º-90º triangle.
All 45º-45º-90º triangles are similar!
They satisfy Angle -Angle (AA) for proving trianlges similar. |
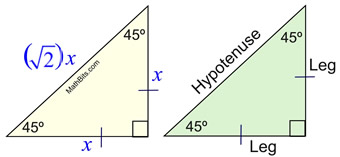
45º-45º-90º is an "Isosceles" Right Triangle |
Our first observation is that a 45º-45º-90º triangle is an "isosceles right triangle". This tells us that if we know the length of one of the legs, we will know the length of the other leg. This will reduce our work when trying to find the sides of the triangle. Remember that an isosceles triangle has two congruent sides and congruent base angles (in this case 45º and 45º).
Create a 45º-45º-90º triangle for investigation: |
Congruent 45º-45º-90º triangles are formed when a diagonal is drawn in a square. Remember that a square contains 4 right angles and its diagonal bisects the angles. If the side of the square is set to a length of 1 unit, the Pythagorean Theorem will find the length of the diagonal to be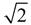 units. units. |
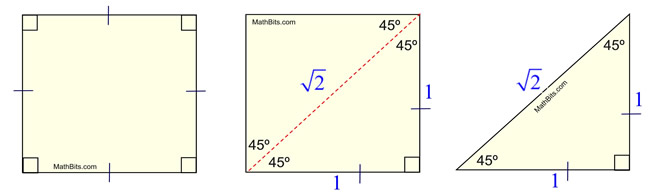 Note: the side of the square need not be a length of 1 for the patterns to emerge.
Note: the side of the square need not be a length of 1 for the patterns to emerge.
The choice of a side length of 1 simply makes the calculations easier.
 |
You have now seen "how" to generate the side lengths of a
45º-45º-90º triangle from a square. If you can remember this relationship, you will be able to tackle any question pertaining to 45º-45º-90º triangles.
|
|
Once the sides of the 45º-45º-90º triangle are established, a series of relationships (patterns) can be identified between the sides of the triangle. ALL 45º-45º-90º triangles will possess these same patterns. These relationships will be referred to as "short cut formulas" that can quickly answer questions regarding side lengths of 45º-45º-90º triangles, without having to apply any other strategies such as the Pythagorean Theorem or trigonometric functions.
|
Short Cut Pattern Formulas: |
Since 45º-45º-90º triangles are similar, their corresponding sides are proportional. As such, we can establish a pattern as to how their sides are related. The following pattern formulas will let you quickly find the sides of a 45º-45º-90º triangle even when you are given only ONE side of the triangle. Remember, these formulas work ONLY in a 45º-45º-90º triangle!
Note: Solving the hypotenuse formula for the leg, gives 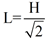 . Remove the radical from the denominator (rationalize),
to get the formula 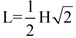 where the answer is already rationalized. You can use either formula to find the leg.
This example shows the application of the patterns when the leg is given.
Always look at what is "given" and what you need to find.
1. |
Find x and y.
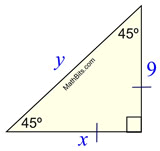
|
x is the "other" leg
(isosceles → legs equal)
No formula needed.
x = 9 Answer
|
y is the hypotenuse
(across from the 90º angle)
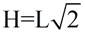
y = 9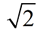 Answer Answer
|
This example shows the application of the patterns when the hypotenuse is given.
Always start with what is "given" and work from that point.
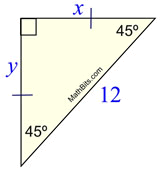
2. |
Find x and y.
|
|
y is the "other" leg
(use the value for x)
No formula needed.
y = 6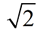 Answer Answer
|
In example 2, if you use the formula 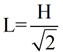 to find the leg, your computations will be to find the leg, your computations will be
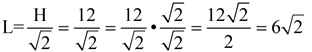 where you need to rationalize the final answer. where you need to rationalize the final answer.
This example requires more work with radicals. For a review on radicals, see Radical Review.
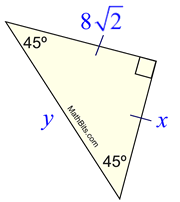
3. |
Find x and y.
|
8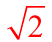 is the leg
(x is the "other" leg) is the leg
(x is the "other" leg)
No formula needed.
x = 8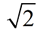 Answer Answer
|
y is the hypotenuse
(use hypotenuse formula)
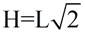
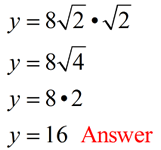
|
 |
Notice that when you are working with a 45º-45º-90º triangle
you are working with 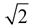 .
Think of the TWO being related to the FOUR: 45, 45, 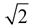 When you work with
30º-60º-90º and 45º-45º-90º triangles,
When you work with
30º-60º-90º and 45º-45º-90º triangles,
you will need to keep straight which radical goes with which triangle.
|
I forgot the formula patterns! Now what?
When working with a 45º-45º-90º triangle, you can always use the Pythagorean Theorem. Unlike the 30º-60º-90º triangle, in a 45º-45º-90º triangle you always know, or can represent, two sides of the triangle.
•
If you know the length of a leg, you know both legs.
• If you know the length of the hypotenuse, represent the legs as x and x.
The Pythagorean Theorem will always work! |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
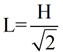 to find the leg, your computations will be
to find the leg, your computations will be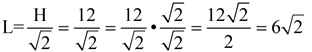 where you need to rationalize the final answer.
where you need to rationalize the final answer.