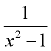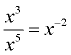|
A polynomial is basically a finite sum of terms (monomials) in which all variables
have
whole number exponents
and no variable appears in a denominator.
 |
A polynomial, of a single variable, is an expression of the form:
|
anxn + an - 1xn - 1 + . . . + a2x2 + a1x + a0
where an ≠ 0, the exponents are all whole numbers,
and the coefficients are all real numbers. |
|
The form shown above is considered "standard form",
with terms starting with the largest exponent
and descending to the smallest exponent.
Example: 4x4 + 2x3 + x2 + 5x + 1 (standard form)
3x5 + 4x3 + 2x - 8 (also standard form -
"missing" terms have coefficient 0)
The degree of a polynomial is the largest exponent within the expression.
Examples: 3x2 + 4x + 1 has a degree of 2. x3 - x2 + 5x - 2 has a degree of 3.
 Knowing the "degree" of a polynomial function will let you determine Knowing the "degree" of a polynomial function will let you determine
the most number of solutions the function may have,
and the most number of times the function will cross the x-axis. |
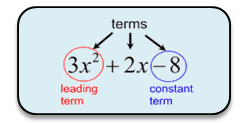
The leading term in a polynomial is the term with the largest exponent.
The constant term in a polynomial is the term without a variable.
In the polynomial definition shown above, an is the leading coefficient,
a0 is the constant term, and n is the degree.

Polynomials: YES or NO |
3x½ |
NO - exponent is not a whole number |
|
NO - the variable is in the denominator |
-3x2 |
YES - satisfies the polynomial definition |
|
NO - the square root of x can be written with a fractional exponent of x being ½. |
2x-3 |
NO - exponent is not a whole number.
Negative exponent places x3 in denominator. |
|
YES - the exponent of x is 1 which is OK.
The coefficient being radical 3 is not a problem. |
Polynomials are one of the foundations of algebra, and have wide applications in various fields of science and engineering. |
|
Classification by Terms |
monomial |
one term: 12, 4x, x2, -5xy |
binomial |
two terms: 2x - 1, x2 - 4 |
trinomial |
three terms: x2 + 2x + 1 |
polynomial - one or more terms: polynomial means "many", but it can also be one term. |
The ending of these words "nomial"
is Greek for "part". |
Classification by Degree |
| Constant: - degree 0: 6 or -2 |
Linear - degree of 1: 3x + 1 or 12 |
Quadratic - degree of 2: 2x2 - x + 7 |
Cubic - degree of 3: 3x3 + 4x2 + 3x + 5
|
| Quartic:- degree of 4: 4x4 + 2x3 + x2 + 5x + 1 |
| Quintic: degree of 5: x5 + x4 + x3 + x2 + x + 1 |
|

 Polynomial Factoring over the Integers: Polynomial Factoring over the Integers:We are most familiar with factoring with respect to integers {..., -3, -2, -1, 0, 1, 2, 3, ...}.
This is the method used to factor "numbers" in elementary school (12 = 2 x 2 x 3).
When you factor, the factors are integers. The example is called "prime factorization".
We have seen this same concept of "factoring over the integers" in beginning Algebra.
x2 - 49 = (x - 7)(x + 7) is "factored over the Integers",
which means that all of the values in the original and resulting polynomials are integers.
But, we have also seen that this concept can be extended to
"factoring over the Real numbers" and "factoring over the Complex numbers."

Keep an open mind when factoring. Not all factors will contain only Integer values. |

 Polynomials and Closure: Polynomials and Closure:
Polynomials form a system similar to the system of integers, in that polynomials are closed under the operations of addition, subtraction, and multiplication.
CLOSURE: Polynomials will be closed under an operation if the operation produces another polynomial.
Adding polynomials creates another polynomial.
Subtracting polynomials creates another polynomial.
Multiplying polynomials creates another polynomial.
Dividing polynomials does not necessarily create another polynomial.
Polynomials are NOT closed under division (since you may get a variable in the denominator). |
The skills of adding, subtracting and multiplying polynomials were developed in Algebra 1.
• Closure under Addition: (2x2 + 3x + 4) + (x2 - 5x - 3) = 3x2 - 2x + 1
When adding polynomials, the variables and their exponents do not change. Only their coefficients will possibly change. This guarantees that the sum has variables and exponents which are already classified as belonging to polynomials. Polynomials are closed under addition.
• Closure under Subtraction: (2x2 + 3x + 4) - (x2 - 5x - 3) = x2 + 8x + 7
In the same manner as described for "addition". we can see that polynomials are closed under subtraction.
• Closure under Multiplication: (x + 1)(x2 + 4x + 3) = x3 + 5x2 + 7x + 3
When multiplying polynomials, the variables' exponents are added, according to the rules of exponents. Remember that the exponents in polynomials are whole numbers. The whole numbers are closed under addition, which guarantees that the new exponents will be whole numbers. Consequently, polynomials are closed under multiplication.
What about division?
Polynomials are NOT closed under division. Look at this simple counterexample:
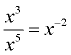 |
When dividing variables with exponents, there is the possibility of creating a negative exponent. Negative exponents are not allowed in polynomials. |
|


(For more information about the similarities between the system of integers
and the system of polynomials, see Polynomials as a System.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|