
 Polynomials form a system similar to the system of integers. Polynomials form a system similar to the system of integers.
The focus of this page is on the relationship between polynomials and integers.
The numbers that we use everyday belong to the decimal number system, or base 10 system.
Every value in our system is based on the number 10. The origins of the use of base 10 are most likely connected with finger counting.
In elementary school, "Base 10 Blocks" are used to help students understand that our numbers (integers in this case) are based upon powers of 10.
The number shown at the right is 1,111.
1000 + 100 + 10 + 1 = 1111
1 x 1000 + 1 x 100 + 1 x 10 + 1x1 = 1111
1 • 10³ + 1 • 10² + 1 • 10¹ + 1 • 10° = 1111
|
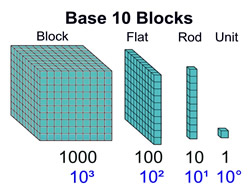 |
The "grouping" blocks of 10's, 100's, and 1000's make representing large quantities easier.
They are also the points at which the powers of 10 increase. |
Let's consider "our" number 372.
Since we know that this number is a base 10 number, we know:
372 = 3 x 100 + 7 x 10 + 2 x 1
372 = 3 • 102 + 7 • 101 + 2 • 100
|
But ... what if we did NOT know that this number was base 10? Since we commonly deal with unknowns in Algebra by using "x", let's replace the base value with an "x":
3 • 102 + 7 • 101 + 2 • 100
3 • x2 + 7 • x1 + 2 • x0
|
 |
|
We just created a polynomial-type value: 3x2 + 7x + 2.
Polynomials may be thought of as representing values in base "x".
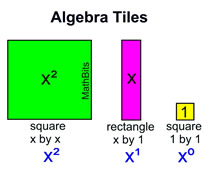
While "Base 10 Blocks" offer a visual presentation of base 10, "Algebra Tiles" are used for a visual presentation of base x, with each different-style tile representing a power of x.
(Cubes are used for x³ and red tiles are used for negative values.)
View this slide show to see Algebra Tiles at work.
|
 |
3x2 + 7x + 2 is represented as: |
|
Please Note: This discussion compares polynomials to the system of integers (not the system of real numbers). When working with number bases, it is possible to represent "decimals" within the base being discussed. For example, in base 10, the number 12.5 = 1 x 101 + 2 x 100 + 5 x 10-1.
This idea of representing "decimals" does not apply to polynomials in base "x", since polynomials do not allow the base value to be raised to a negative exponent. Thus, the polynomial comparison is to the system of integers only.
FYI: While we know and love base 10 values, there are other number bases at work around us. Base 2 (binary number system) and base 16 (hexadecimal number system) are frequently used in computer science. Even the numbers used to specify the colors you see on this HTML web page use a hexadecimal system ("000000" is black and "ffffff" is white). Yes, there are letters in the hexadecimal system.
(For more information about working with number bases, view:
number bases; converting from base 10; converting to base 10; converting via base 10.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|





