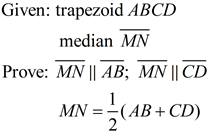
Proof for Theorem
Prove: The median of a trapezoid is parallel to the bases and equal in length to half the sum of the bases.
trapPfGiven
thtrapmed
 
Statements
  
Reasons
1.
trapPf1
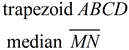1.
Given
2.
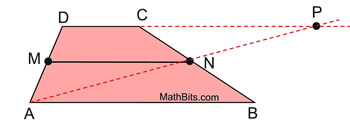
Draw an, extending until it intersects with extension of dc, at P.
2.
Two points determine exactly one line.
3.
trapPf3
M midpoint ad
3.
A median of a trapezoid joins the midpoints of the legs.
4.
trapPf4
4.
Midpoint of a segment forms two congruent segments.
5.
trapPf5
5.
Trapezoid has at least one pair of parallel sides.
6.
∠ABNcongruent∠PCN
6.
If 2 || lines are cut by a trans., the alternate interior ∠ are congruent.
7.
∠ANBcongruent∠PNC
7.
Vertical ∠s are congruent.
8.
trapPf8
8.
ASA-if 2 ∠s and the included side of 1 Δ are congruent to the corres. parts of other Δ, the Δs are congruent.
9.
trapPf9; trapPf99
9.
CPCTC-corres partscongruentΔs arecongruent
10.
N is midpoint of ap
10.
Midpoint of a segment forms two congruent segments.
11.
mnmid-segment ΔADP
11.
Mid-segment of Δ joins midpts of two sides of Δ.
12.
trapPf12*
12.
Mid-segment of Δ is parallel to the third side of the Δ.
13.
trapPf13*
13.
If 2 lines are || to the same line, they are || to each other.
14.
 MN = ½ DP; (2MN = DP)
14.
 Mid-seg. of Δ=½ of 3rd side.
15.
 DP = CP + DC
15.
 Segment Add. Postulate
16.
 AB = CP
16.
 congruentsegments have = length.
17.
 DP = AB + DC
17.
 Substitution
18.
 2MN = AB + DC
18.
 Substitution
19.
 MN = ½ (AB + DC)*
19.
 Division

All Rights Reserved - Copyright MathBitsNotebook.com