Proof for Theorem
Prove: If a trapezoid has congruent diagonals, it is an isosceles trapezoid.
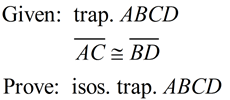thisos5given thisos5a
 
Statements
  
Reasons
1.
trap. ABCD
thisos2pf7
1.
Given
2.
Draw cpthrough C || to db intersectsabextended at P.
2.
Through a pt. not on a given line, only one line may be drawn || to the given line.
3.
thisos2pf3
3.
A trap. is a quad. with at least 1 pr. of parallel sides.
4.
BPCD is parallelogram
4.
A parallelogram has 2 sets of parallel sides.
5.
thisos54
5.
Parallelogram has opposite sides congruent.
6.
thisos55
6.
Transitive (or substitution)
7.
ΔACP is isosceles
7.
Isosceles Δ has 2 congruent sides.
8.
∠CABcongruent∠CPB
8.
Base ∠s of isos.Δ are congruent.
9.
∠CPBcongruent∠DBA
9.
If 2 || lines are cut by a trans., the corres. ∠s are congruent.
10.
∠CABcongruent∠DBA
10.
Transitive (or substitution)
11.
thisos2pf5
11.
Reflexive property.
12.
thisos512
12.
SAS-if 2 sides and the included ∠ of one Δ are congruent to the corres. parts of another Δ, the Δs are congruent.
13.
 ∠DAB congruent ∠CBA
13.
CPCTC-corres. partscongruentΔs arecongruent.
14.
isos. trap. ABCD
14.
Def: An isosceles trapezoid is a trapezoid with congruent base angles.

All Rights Reserved - Copyright MathBitsNotebook.com