Proof for Theorem (converse)
Prove: If a parallelogram has diagonals bisecting the angles, it is a rhombus.
Prove: If a parallelogram has diagonals bisecting the angles, it is a rhombus.
 |
 |
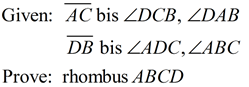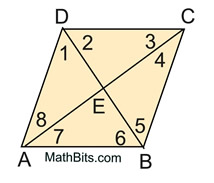Statements |
Reasons |
||
1. |
  |
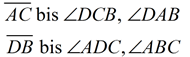1. |
Given |
2. |
 |
2. |
An angle bisector is a ray in the interior of the ∠ forming 2  ∠s. |
3. |
 |
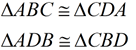3. |
Diagonal of a parallelogram forms two congruent triangles |
4. |
 |
4. |
CPCTC - corres. parts of triangles are . |
5. |
 |
5. |
Transitive property |
6. |
 |
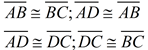6. |
If 2 ∠s of a triangle are , the sides opposite are . |
7. |
 |
7. |
Transitive property |
8. |
rhombus ABCD |
8. |
A rhombus is a parallelogram with 4 congruent sides. |
All Rights Reserved - Copyright MathBitsNotebook.com