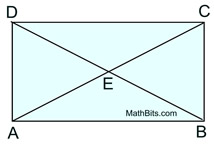
Proof for Theorem
Prove: If a parallelogram has congruent diagonals,
it is a rectangle.
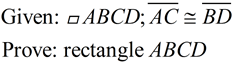QD2given
QDrect1
 
Statements
  
Reasons
1.
!Drect2
1.
Given
2.
QDrect22
2.
A parallelogram has 2 sets of opposite sides parallel.
3.
QDrect23
3.
Opposite sides of a parallelogram are congruent.
4.
QDrect24; QDrect44
4.
Reflexive property
5.
QDrect16
QDrect55
5.
SSS-if 3 sides of one triangle are congruent to the corres. parts of the other, the triangles are congruent.
6.
∠DAB congruent ∠CBA
∠ADC congruent ∠BCD
6.
CPCTC- corres. parts of congruent triangles are congruent.
7.
∠DAB supp ∠CBA
∠ADC supp ∠BCD
7.
If 2 || lines are cut by a trans., the interior ∠s on same side of trans. are supplementary.
8.

m∠DAB + m∠CBA = 180
m∠ADC + m∠BCD = 180
8.
Supp. ∠s are 2∠s the sum of whose measures is 180º.
9.
m∠DAB = m∠CBA
m∠ADC = m∠BCD
9.
congruent ∠s are ∠s of = measure.
10.
m∠DAB + m∠DAB = 180
m∠ADC + m∠ADC = 180
10.
Substitution
11.
2m∠DAB = 180
2m∠ADC = 180
11.
Addition
12.
m∠DAB = 90
m∠ADC = 90
12.
Division
13.
∠DAB, ∠CBA right ∠s
∠ADC, ∠BCD right ∠s
13.
A rt. ∠ has a measure of 90º
14.
rectangle ABCD
14.
A rectangle is a parallelogram with four right angles.

All Rights Reserved - Copyright MathBitsNotebook.com