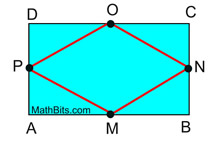
Proof 1
Prove: The figure formed by connecting, in order, the midpoints of the sides of a rectangle is a rhombus.
proof1given
QDproof1
se
 
Statements
  
Reasons
1.
proof11
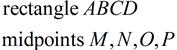1.
Given
2.
pf1
2.
A rectangle is a parallelogram.
3.
proof13
3.
Opposite sides of a parallelogram are congruent.
4.
∠A, ∠B, ∠C, ∠D rt. ∠s
4.
A rectangle has 4 rt. ∠s.
5.
 ∠Acongruent∠Bcongruent∠Ccongruent∠D
5.
 All right ∠s are congruent.
6.
proof16
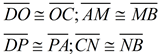6.
Midpoint of a segment forms 2 congruent segments.
7.
DC = DO + OC
AB = AM + MB
DA = DP + PA
CB = CN + NB
7.
Segment addition postulate (or whole quantity = sum of parts).
8.
DC = AB; DA = CB;
DO = OC; AM = MB;
DP = PA; CN = NB
8.
congruentsegments have = length
9.

AM + AM = DO + DO
DP + DP = CN + CN

9.
Substitution
10.
2AM = 2 DO; 2DP = 2CN
10.
Addition
11.
AM = DO; DP = CN
11.
Division
12.
AM = DO = OC = MB
DP = CN = PA = NB
12.
Substitution
13.
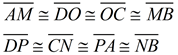proof113
13.
congruentsegments have = length
14.
proof1144
14.
SAS - if 2 sides and included < of 1 Δ are congruent to the corres. parts of another, the Δs are congruent.
15.
proof115
15.
CPCTC - corres. parts of congruent Δs are congruent.
16.
proof116
16.
A qaud. with 2 sets of opposite sides congruent is a parallelogram.
16.
rhombus MNOP
16.
A rhombus is a parallelogram with 4 congruent sides.

All Rights Reserved - Copyright MathBitsNotebook.com