Practice Page
Directions: Read carefully. Choose the best answers.

1.
Evaluate the following:
a) 5!       b) 8P3       c) 0!       d) 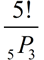perm1P
Choose:
 
120, 168, 1, 2
120, 336, 1, 2
 
120, 84, 1, 5
120, 168, 0, 5
perp1
  

 

 

2.
How many different 5-letter arrangements are there of the letters in the word moose?
perp2

Choose:
 
120
60
 
30
20

 

 

3.
How many different seven-letter arrangements of the letters in the word HEXAGON can be made if each letter is used only once?
perp3
Choose:
 
28
49
 
720
5040

 

 

4.
Two cards are drawn at random from a standard deck of cards, without replacement. Find the probability of drawing an 8 and a queen in that order.
perp4
Choose:
 
4/52
4/2652
 
8/2652
16/2652

 

 

5.
Crystal is making personalized invitations for a party. The party-goers are Hallie, Alex, Edward, Alison, Matt, Aleia, Kyle, and Lacey. What is the probability that if Crystal selects a name at random that she will pick a name starting with the letter "A" or the letter "L"?

perp5
Choose:
 
2/8
3/8
 
4/8
6/8

 

 

6.
There are 12 horses in a horse show competition. The top three winning horses receive money. How many possible money winning orders are there for a competition with 12 horses?
perp66
Choose:
 
36
120
 
1200
1320

 

 

7.
Fred is lining up his four golf trophies on a shelf. How many different possible arrangements can he make?
perp7
Choose:
 
24
16
10
4

 

 

8.
A password consists of three digits, 0 through 9, followed by three letters from an alphabet having 26 letters. If repetition of the digits is allowed, but repetition of the letters is not allowed, determine the number of different passwords that can be made.
perp8
Choose:
 
4,368,000
11,232,000
 
15,600,000
18,560,000

 

 

9.
Six members of a school’s varsity fencing team will march in a parade. How many different ways can the players be lined up if Josh, the team captain, is always at the front of the line?
perp9
Choose:
 
750
360
 
120
60

 

 

10.
License plates are formed using four letters followed by a three-digit number without repetition of either letters or digits. Zero may be chosen as the first digit of the number. How many license plates can be formed under this pattern?
perp10
Choose:
 
56,750,000
175,760,000
 
180,835.200
258,336,000

 

 

11.
Determine whether the following situations would require calculating a permutation or a combination:
a) Selecting five students to attend a State conference.
permutation     combination

b) Selecting a first play winner and a second place winner.
permutation     combination

c) Assigning students to their seats on the first day of school.
permutation     combination

 

 

 

 

12.
A customer selects three different toppings for a pizza. If there are 9 different toppings from which to choose, how many different pizzas can be made?
perp12
Choose:
 
12
27
 
84
504

 

 

13.
A teacher chooses a committee of 5 students from the class of 25 students. How many different committees can be chosen?
perp13
Choose:
 
53,130
6,375,600
 
106,260
3,187,800

 

 

14.
There are 12 juniors and 20 seniors in the Debate Club. If the members decide to send a team of 2 juniors and 3 seniors to a Debate Conference, how many different conference teams are possible?
perp14
Choose:
 
46,200
75,240
 
84,560
108,240

 

 

15.
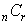If f represents the number of combinations of n items taken r at a time,
what is the value of 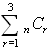d if n = 4 ?
 perp15
Choose:
 
24
14
 
6
4

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".