 |
Quadratic: Involving terms of the second degree at most.
Parabolas (y = x2 - 4x - 2) and circles (x2 + y2 = 16) are quadratics.
|
|
A linear quadratic system is a system containing one linear equation and one quadratic equation.
Linear-Quadratic System
Line - Parabola
y = x - 2
y = x2 - 4x - 2 |
Linear-Quadratic System
Line - Circle
2y = x +1
x2 + y2 = 1
|
In Algebra 1, we worked with linear-quadratic systems that contained straight lines and parabolas. Both algebraic and geometric solutions were developed.
The possibility of the linear systems containing "lines and circles" was mentioned.
In Geometry, we are going to concentrate on graphical solutions for linear-quadratic systems whose components are a straight lines with EITHER a parabola or a circle
(with emphasis on circles since you are already familiar with parabolas).

REFRESH:
Linear-Quadratic System: linear equation and parabola
(only one variable is squared) |
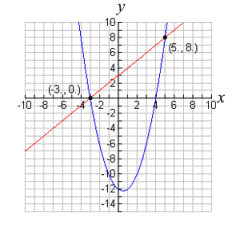
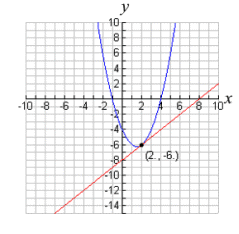
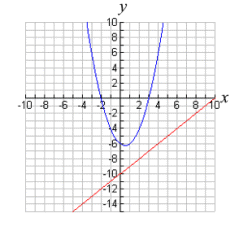
This familiar linear-quadratic system, has only one variable being squared, and will be the graph of a straight line and a parabola. The graphs below show that when a line and a parabola are graphed on the same set of axes, three situations are possible.
 |
 |
 |
| The equations will intersect in two locations.
Two real solutions. |
The equations will intersect in one location. One real solution. |
The equations will not intersect.
No real solutions. |

By hand:
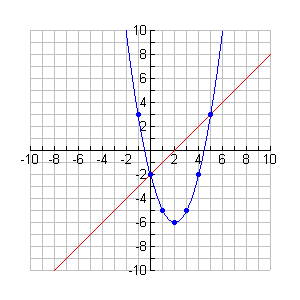
Solve by graphing:
y = x - 2
y = x2 - 4x - 2
To check: place the solution coordinates into each equation. |
Use axis of symmetry to establish the turning point for the parabola:
x = -b/2a = -(-4)/2(1) =2
x = 2 turning point at (2,-6)
| x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
| y |
3 |
-2 |
-5 |
-6 |
-5 |
-2 |
3 |
Use y = mx + b for line graph.
m = 1, and b = -2
Solution: {(0,-2), (5,3)} |
 |
In the Example above, we were lucky in that the intersection points gave us integer coordinates.
That is not always the case. If you are unsure of the solution (or your solution does not check), graph your graphing calculator and see what the solution should actually be.
We will use the example above to show what to do to "check" on the graphing calculator.

By calculator:
Solve by graphing:
y = x - 2
y = x2 - 4x - 2
Solution:
{(0,-2), (5,3)}
|
First, graph the equations. Be sure your viewing window shows a clear picture of the parabola and the line.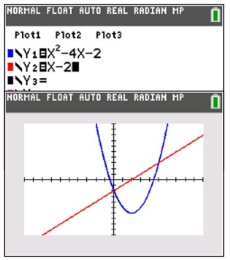
Notice, in the first graph in the next column, that the x-value is 2.37E-15. This is actually 0.
Consider pushing the decimal point 15 places to the left.
0.000000000000002.37
|
Use the INTERSET option twice to find the two locations where the graphs intersect (the answers).
2nd TRACE (CALC)#5 intersect
Move spider close to the intersections. Hit ENTER 3 times.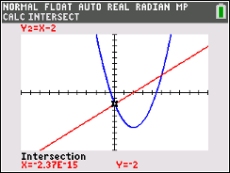 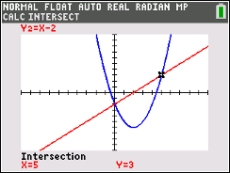 |

Linear-Quadratic System: linear equation and circles
(two variables are squared) |
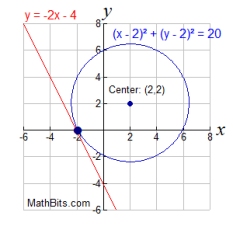
Let's take a look at a linear-quadratic system, having two variables squared, where one equation is a line and the other is a circle. Like with the parabola, the graphs below show that when a line and a circle are graphed on the same set of axes, three situations are possible.
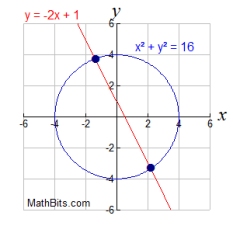 |
 |
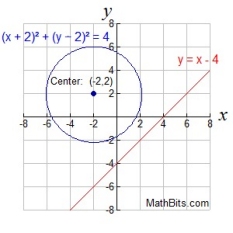 |
| The equations will intersect in two locations.
Two real solutions. |
The equations will intersect in one location (a tangent). One real solution. |
The equations will not intersect.
No real solutions. |

By hand:
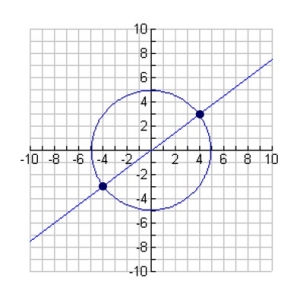
Solve by graphing:

|
For a refresher on plotting circles, click here.
This circle has a center at the origin with a radius of 5.
Use y = mx + b for line graph.
m = ¾, and b = 0.
Solution: {(-4,-3), (4,3)}
To check: place the solution coordinates into each equation. |
 |
Again, we were lucky to have the solutions be integer coordinates.
So, if a solution point is not comprised of integers, and your solution does not check, you can solve algebraically to find the coordinates. Let's see how that can be done.
Algebraic Solution:
Solve:

We will be substituting the "y =" value into the second equation to solve for x.
Solution:
{(-4,-3), (4,3)}
|
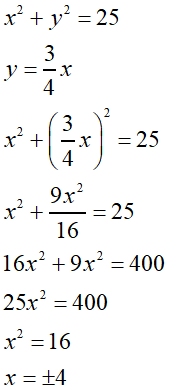
The x-coordinates of the solutions will be +4 and - 4.
(4, __) and (-4, __)
|
Find the missing y-values by substituting the +4 and -4.
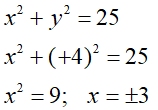
The result is the same for both +4 and -4.
We know, from the graph, that the x = -4 is in the third quadrant, so we have
(-4,-3).
And likewise, since the x = +4 is in the first quadrant, we have (4,3).
|
Because of the difficulty in graphing "complete" circles on the graphing calculator,
it can be challenging to find a linear quadratic solution when working with a line and a circle on the graphing calculator. Click here (or below) to see how it can be done.