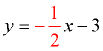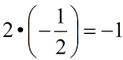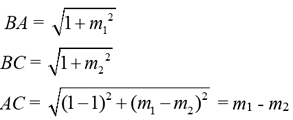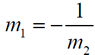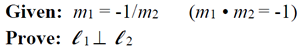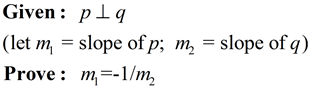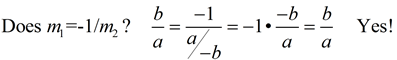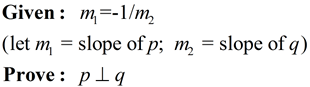|
When lines intersect, the angles created by the intersection can be a valuable piece of information regarding the conditions surrounding the intersection point. Probably the most popular intersection angle is the 90º angle which creates perpendicular lines.
Let's continue our investigation of lines by examining perpendicular lines.
|
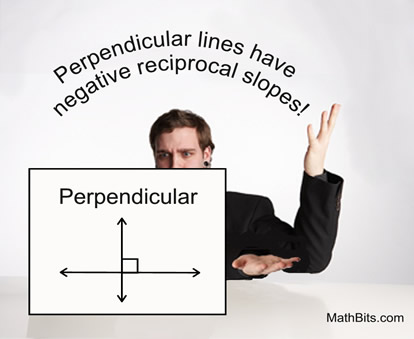
Perpendicular lines are two coplanar lines that intersect at a right angle (90º). |
|
We know that a relationship exists between the slopes of parallel lines (the slopes are equal).
There is also a relationship between the slopes of perpendicular lines (the slopes are negative reciprocals)
Non-vertical perpendicular lines have negative reciprocal slopes!
(The product of the slopes is -1.) |
Why did we specify "non-vertical" perpendicular lines?
In the coordinate plane, all vertical lines are parallel to the y-axis and all horizontal lines are parallel to the x-axis. These vertical and horizontal lines are perpendicular to one another. But, expressing their slopes as negative reciprocals is not mathematically possible. The slope of vertical lines is undefined, and the negative reciprocal of a horizontal line (slope 0) is also undefined.
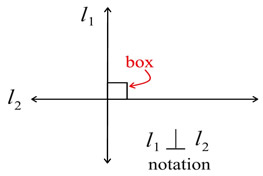
Perpendicular lines are marked with "a box" to indicate the location of the right angle.
Perpendicular lines intersect in one location, which becomes the vertex of the right angle.
Remember that a right angle contains 90º (think of the angle in the corner of a square).
|
 |
To find the negative reciprocal of a number,
flip the number over (take the reciprocal or invert)
and negate that value.
Number:
|
Negative Reciprocal: |
3
(3 is 3 over 1) |
|
|
|
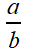 |
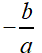 |
Equations of Lines:
y = 2x + 1
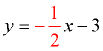 |
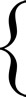 |
These lines are perpendicular since their slopes are negative reciprocals.
The negative reciprocal of 2 is 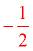 . |
|
If you multiply a slope times its negative reciprocal, the result is always -1.
|
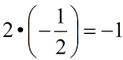 |
|

|
Slope Criteria for Perpendicular Lines:
Let's prove that perpendicular lines have negative reciprocal slopes, AND that negative reciprocal slopes imply perpendicular lines. We will look at a "Geometric/Algebraic Proof" and a "Transformational Proof".
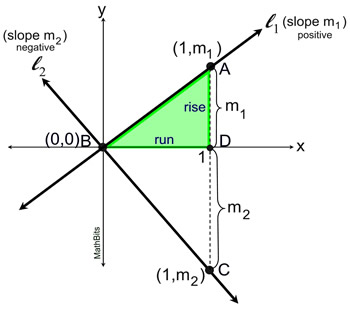
Geometric/Algebraic Proof: |
|
If two lines are perpendicular, the slopes are negative reciprocals.
(The product of the slopes = -1.) |
|
Vertical lines will not be considered since their slopes are undefined. Also, horizontal lines will not be considered
since their slopes of 0 have undefined reciprocals. Vertical and horizontal lines are perpendicular.

 |
Since we are trying to establish a connection between perpendicular lines and negative reciprocal slopes, we will need to also prove the converse of the theorem stated above. In this manner, we will connect perpendicular lines to negative reciprocal slopes AND negative reciprocal slopes to perpendicular lines. |
|
If the slopes of two lines are negative reciprocals, the lines are perpendicular. |
|

|
If two lines are perpendicular, the slopes are negative reciprocals.
(The product of the slopes = -1.) |
|
Vertical lines will not be considered since their slopes are undefined. Also, horizontal lines will not be considered
since their slopes of 0 have undefined reciprocals. Vertical and horizontal lines are perpendicular.
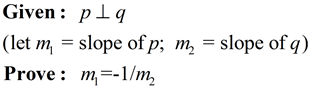
We will be using a 90º rotation to complete this proof.
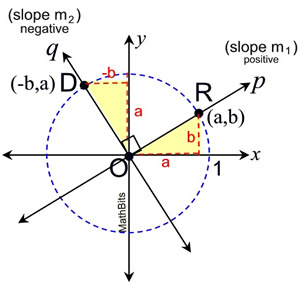
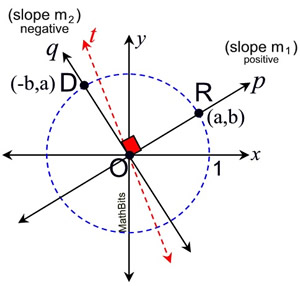
• For visualization, a unit circle (centered at O, radius 1) is drawn, intersecting line p at point R and line q at point D. (Any circle centered at O can be used to visualize the rotation.) |
|
| • Rotate point R 90º counterclockwise about the center of the rotation O. Since p and q are perpendicular, the image (point D) will lie on line q under this 90º counterclockwise rotation.
• Since this rotation maps the positive x-axis to the positive y-axis, and the positive y-axis to the negative x-axis, we know that the coordinates of R(a,b) are transformed into the coordinates of D(-b,a). Graphically, you can see the movement of lengths a and b under the rotation.
• Examining "rise" and "run", m1 (slope of p) is 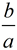 , and m2 (slope of q) is , and m2 (slope of q) is 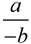 . .
• 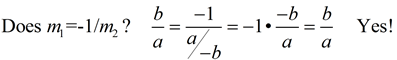
• The slope of line q is the negative reciprocal of the slope of line p.

|
 |
As was done in the Geometric/Algebraic Proof, we need to also prove the converse of the theorem. In this manner, we will connect perpendicular lines to negative reciprocal slopes AND negative reciprocal slopes to perpendicular lines. |
|
If the slopes of two lines are negative reciprocals, the lines are perpendicular. |
|
Vertical lines will not be considered since their slopes are undefined. Also, horizontal lines will not be considered
since their slopes of 0 have undefined reciprocals. Vertical and horizontal lines are perpendicular.
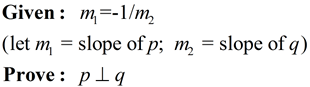
We will be examining a line t that IS perpendicular to p at point O, and showing that line t must actually be line q.
• If m1 = -1/m2, we know that one of the slopes is positive and one slope is negative. The lines p and q meet in a single point, O.
|
|
| • There exists some line, t, through O which is perpendicular to line p.
• From our previous proof, we know that the slope of line p will be the negative reciprocal of the slope of t. If we let mt = the slope of t, we know m1 = -1/mt
• By substitution we have: -1/m2 = -1/mt . And we now know m2 = mt .
• Since line t and line q have the same slope and pass through the same point, they are the same line (t = q).
• Since p is perpendicular to t, we know p is perpendicular to q.
(Remember from your work with constructions that from a point on a line (O on p), one and only one perpendicular, q, can be drawn.) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|