Let's make some observations about the general form of a circle.
There are some interesting connections that pop up in this form.
General Form of a Circle:
x2 + y2 + Cx + Dy + E = 0 |
|
Is there a relationship between the coordinates of the center of a circle and the values of C and D in the general form of a circle? Take a look!
General Form |
Center-Radius Form |
x2 + y2 + 2x - 4y - 11 = 0
C = 2, D = -4
|
(x + 1)2 + (y - 2)2 = 16
Center (-1,2) |
x2 + y2 - 4x - 6y + 8 = 0
C = -4, D = -6 |
(x - 2)2 + (y - 3)2 = 5
Center (2,3) |
|
 |
It appears that the values of C and D are (-2) times the coordinates of the center respectively.
Is this really occurring?
When (x + 1)2 + (y - 2)2 = 16 is expanded, (x + 1)2 becomes x2 + 2x + 1,
where the center
term's coefficient doubles the value of +1.
While the equation deals
with (x + 1)2, the actual x-coordinate of the center of this circle is (-1).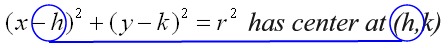
Yes, this relationship is occurring!

Now, let's see if this relationship will allow us to establish any other relationships regarding the general form of a circle and the center-radius form.
Let the center of the circle be (-p, -q).
We now know C = (-2)(-p) = 2p and D = (-2)(-q) = 2q, so we have:
x2 + y2 + 2px + 2qy + E = 0
If we complete the square on this equation, we will make a discovery about the radius.
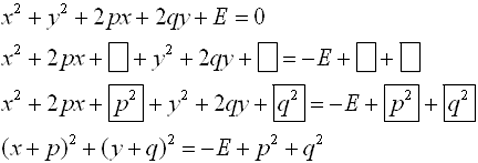 |
Center: (-p,-q)
Radius: 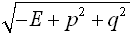 |
We have now found a relationship between the general form of the equation and radius.
Radius: 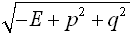
Remember, you have already seen how to find the center of the circle from the general form of the equation.
So, now we have a way to obtain the center and the radius directly from the general form of the equation of a circle.
Is this easier than completing the square to get the center-radius form of the equation to get the center and radius? Probably not, since you would have to remember these relationships.
But, isn't it amazing what a little investigating and a little algebra can uncover!
|