Under Constructions, we saw a geometric method for finding the center of a circle by drawing an inscribed angle and then constructing the perpendicular bisectors of the sides of the angle.
That inscribed angle actually determined three points that lie on the circle.
On this page, we are going to:
locate the center of a circle given only three points
on the circle, using slopes and equations.
|
|
In Part I, we will establish the process in a generalized form using variable representations.
In Part II, we will show a numeric based application.
Part I: General Form
The three points on the circle are labeled
Draw a line through points A and B, labeled r.
Draw a line through points B and C, labeled t.
Write the equations of these two lines: |
 |
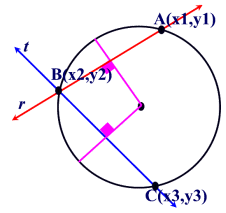Geometrically, we know that the center of the circle will lie on lines that pass through
the midpoints of chords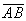 
and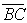 
and are perpendicular to each chord.
Lines that are
perpendicular have negative reciprocal slopes.
We will call these new lines rp and tp to indicate their perpendicular connection to lines r and t.
Write equations for the perpendicular lines passing through the midpoints:
Solve for x:
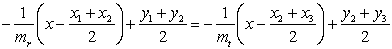
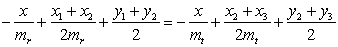
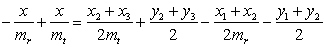
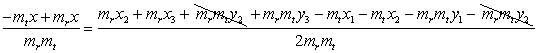
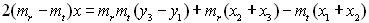
Once we have the formula for finding x, we can just substitute into one of the line equations for the perpendiculars to find the y value of the center. Whew!!
The radius can be found using the distance formula with the center and any of the points. |
)
