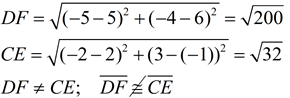Proof for Problem 5

Given: quadrilateral CDEF with
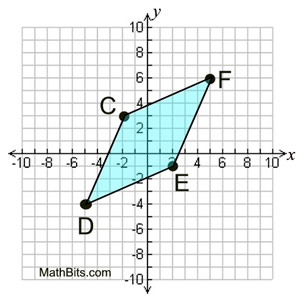
C(-2,3), D(-5,-4), E(2,-1) and
F(5,6)

Prove: CDEF is a rhombus but not a square

PROOF: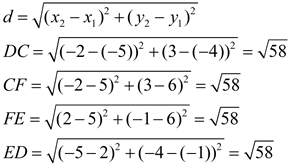
showans5
proofshow5

showans5a
CDEF is a parallelogram because it has 2 sets of opposite sides congruent. It is a rhombus because it has four congruent sides.showans5b
CDEF is not a square because a square has congruent diagonals and the diagonals of CDEF are not congruent.

All Rights Reserved - Copyright MathBitsNotebook.com