Using Constructions 8
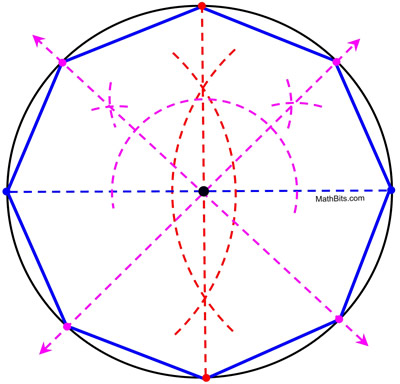
We have already seen how inscribing a square in a circle, divides the circle into four equal arcs. Since we need 8 equal arcs for a regular octagon, we will start by dividing the circle into 4 sections and then bisect these sections to form 8 sections.
1. Start with a given circle with center indicated.
2. Draw a diameter and construct the perpendicular bisector of the diameter. This will divide the circle into 4 equal arcs.
3. Bisect the angle forming one of the quadrants. Extend the angle bisector to a line passing completely through the circle.
4. Repeat this angle bisecting process for an adjacent quadrant.
5. Connect the 8 intersection points on the circle to form a regular octagon.
Note that the initial bisecting of the right angles forms 45º angles which are the central angles of a regular octagon.
All Rights Reserved - Copyright MathBitsNotebook.com