Formulas for Geometric Sequences and Series
and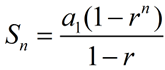   

The origin of the formula to find a specific term of a geometric sequence where the common ratio of successive terms is r can be seen by examining the sequence pattern.

Notice that the exponent of r is one less than the location of the term.
Thus we have

___________________________________________________________________________

If we carry this idea further, we can find the formula for partial sums of a geometric sequence.
First express the series in a manner similar to what was done with the "Pattern" above:

Now, multiply both sides by the common ration r:

Now, subtract these two equations and notice values that disappear. We will end up with:

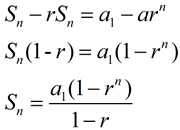
All Rights Reserved - Copyright MathBitsNotebook.com