Formulas for Arithmetic Sequences and Series
  and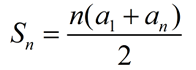  

The origin of the formula to find a specific term of an arithmetic sequence where the common difference between terms is d can be seen by examining the sequence pattern.

Notice that the coefficient of d is one less than the location of the term.
Thus we have

___________________________________________________________________________

If we carry this idea further, we can find the formula for partial sums of an arithmetic sequence.
First examine the terms, as we did above, starting with the first term.

Now, try the same approach starting with the last term, and working backward.

This process of comparing a sequence forward and backward is credited to Carl Gauss.
Read about his story.

Now, add these two equations together and notice values that disappear. We will end up with:

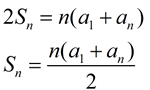
All Rights Reserved - Copyright MathBitsNotebook.com