Answer Box

• State the roots of the polynomial
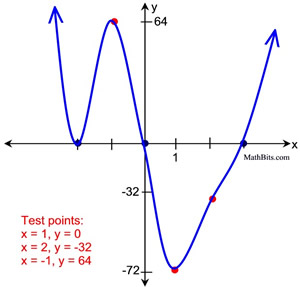
P(x) = x (x + 2)² (x - 3)³.
Roots: (set factors equal to zero)
x = 0; x = -2; x = -2; x = 3; x = 3; x = 3
• Indicate whether the graph crosses the x-axis at each root, or just touches the x-axis.
At x = 0, multiplicity 1 means crosses.
At x = -2, multiplicity 2 means touches.
At x = 3, multiplicity 3 means crosses.
• Draw a sketch of the graph.
Leading coefficient will be positive and the degree is even (degree 6). Therefore, end behavior has both ends pointing up.
Since the equation is known, test points can be used to enhance the sketch.

Do not assume test points are relative maxima or minima unless you test small intervals (neighborhoods) surrounding the point. In this problem, the actual relative maximum and minimum points are:
relative maximum
(0.9201342, 64.63884)
relative minimum
(1.0867998, -72.51832)