Answer Box

The polynomial P(x) = 2x³ + 4x² - 14x + 8 has (x + 4) as a factor.
a) Factor the polynomial into three linear terms.
Use division (any method) to help find the other factors.

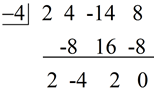By synthetic division, we get
P(x) = (x + 4)(2x² - 4x + 2) = 2(x + 4)(x² - 2x + 1)
= 2(x + 4)(x - 1)(x - 1) [3 linear factors]

b) Describe the end behavior. The degree of this polynomial is odd and the leading coefficient is positive. The end behavior will be left down and right up.
c) Identify all intercepts. The x-intercepts are at the root values of
x = -4, and x = 1, making the intercepts (-4,0) and (1,0).
The y-intercept is where x = 0, which is the point (0,8).
d) Describe how you would go about sketching the graph of a function defined by this polynomial.
Plot the two x-intercepts at x = -4 and x = 1. Notice that the multiplicity of (x - 1) is two and the multiplicity of (x + 4) is one. The graph will only touch the x-axis at x = 1 and it will cross the x-axis at x = -4. Using the end behavior, a rough sketch can be drawn. Test points could be used to enhance the sketch.