|
|
A coordinate graph (often referred to as a coordinate axes or coordinate grid), is a two-dimensional number line where the two lines are perpendicular to one another.
• The horizontal axis is the x-axis.
• The vertical axis is the y-axis.
• A location in the grid is referred to as an ordered pair (or as "the coordinates").
• The point where the axes intersect is called the origin labeled with ordered pair (0,0).
• An ordered pair lists the x-axis value first, followed by the y-axis value in the form (x, y).
• The axes in a coordinate grid form four sections called quadrants (quadrants I, II, III and IV).
|
|
|
Plotting points on a coordinate grid:
Remember that an ordered pair is in the form (x,y).
• first move left or right on the x-axis.
• then move up or down on the y-axis.
• plot the point where these locations intersect.
• label the point using an ordered pair (x, y)
|
Reflections of points:
Did you notice that the points (-3,4) and (3,4), on the grid above, are reflections of one another over the y axis?
When two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
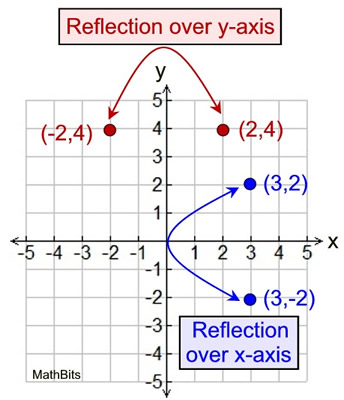 |
Reflection over y-axis:
When a point is reflected over the y-axis, the x-coordinate changes its sign.
(2,4) becomes (-2,4) or vice versa
Notice that the
point and its reflection are both two units horizontally away from the y-axis.
Reflection over the x-axis:
When a point is reflected over the x-axis, the y-coordinate changes its sign.
(3,2) becomes (3,-2) or vice versa
Notice that the
point and its reflection are both two units vertically away from the x-axis.
|
Reflection over both axes:
A reflection over both axes is a combination of a reflection over the x-axis and a reflection over the y-axis (in either order).
Following the pattern shown at the right, the point (2,3) is first reflected over the x-axis, and is then reflected over the y-axis. The ending point, (-2,-3), is a reflection over both axes.
In a reflection over both axes, both coordinates change their signs.
|
 |
|
Distance Between Points:
When working on a coordinates axes, the distance between points with the same x-coordinate or the same y-coordinate can be easily determined by counting the vertical segment units or horizontal segment units separating the points.
Remember that distance is always a positive quantity (or zero).
On the graph at the right, the distance from point A to point B can be counted to be 6 units.
Since we are determining horizontal distance, we are examining the change in the x-coordinates. We are looking to find the distance from x = -4 to x = 2.
On a number line, we can count the distance from -4 to 2 and get 6 (which is essentially how we counted on the grid).
We can also represent this concept using absolute value. |
|
Under Absolute Value, we saw that the distance between two values a and b can be
expressed
as | a - b | or | b - a |. Applying this information to finding the distance from point A to point B, we we examine the x-coordinates and get | -4 - 2 | = 6 or | 2 - (-4) | = 6.
This same approach can be used to find the distance from point C to point D. Since this distance is vertical, we are examining the y-coordinates. We need to find the distance from y = 1 to y = -3.
By counting, we find this distance to be 4 units.
Using absolute value, we have | 1 - (-3) | = 4 or | -3 - 1 | = 4.
But what happens if the distance between the points is "diagonal" instead of vertical or horizontal (such as the distance from A(-4,3) to C(4,1))?
We will have an answer to this question when we develop a friendship with the Pythagorean Theorem under the Geometry section. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|