Examining Integers on a Number Lines: |
Integers are the numbers that belong to the set {... , -3, -2, -1, 0, 1, 2, 3, ...}.
 Plotting Integers on the Number Line: Plotting Integers on the Number Line:
Plot 4 on a number line and indicate the location of its opposite.

The integer 4, and its opposite (-4), are each four units from zero.

 Order of Integers on the Number Line: Order of Integers on the Number Line:

Observations:
• As you move from left to right on a number line, the number values get larger.
-9 < -4 -4 < 0 0 < 4 4 < 7
The numbers are getting bigger as you move to the right.
• Positive numbers are always larger than negative numbers.
• Zero is less than a positive number, but greater than a negative number.
• As you move from right to left on a number line, the number values get smaller.
7 > 4 4 > 0 0 > -4 -4 > -9
The numbers are getting smaller as you move to the left.
Hint: When determining which of two negative numbers is larger (or smaller), picture them on the number line. The number to the right will be larger. The number to the left will be smaller.
When interpreting an inequality, look at the positions of the numbers on the number line. |

Examining Rationals on a Number Lines: |
Rationals are the set of numbers that are fractions whose numerators and denominators are integers (no denominators of zero).
This set includes terminating and repeating decimals which can be expressed as fractions.
All of the situations shown above, regarding integers, will also apply to rational numbers. Remember that the rational numbers include the integers. Rationals, however, open the door for more types of numbers to also be examined. All rational numbers have their place on the number line. Number lines may be divided into fractional parts, or into decimal parts, to show locations of rational numbers.
 Plotting Rationals on the Number Line: Plotting Rationals on the Number Line:
 Plot Plot 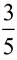 on a number line and indicate the location of its opposite. on a number line and indicate the location of its opposite.
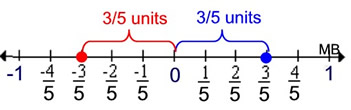 |
Notice how the interval was divided into fractional parts that were the same denominator as that of the desired fraction to be plotted. |
Just as was done with integers, the opposite of the fraction
is the same distance in the opposite direction from zero.
We can see from the number line that
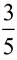 is between 0 and 1,
and its opposite is between 0 and -1.

 Plot 1.4 on a number line and indicate the location of its opposite. Plot 1.4 on a number line and indicate the location of its opposite.


 Plot 4.5 and 9.2 on a number line and indicate the location of their opposites. Then determine the distance between 9.2 and the opposite of 4.5. Plot 4.5 and 9.2 on a number line and indicate the location of their opposites. Then determine the distance between 9.2 and the opposite of 4.5.
If your number line is not subdivided into fractional parts, or decimal parts, you may have to make your best approximation as to where the points will lie (between the markings on the number line you are given). See the plotting below.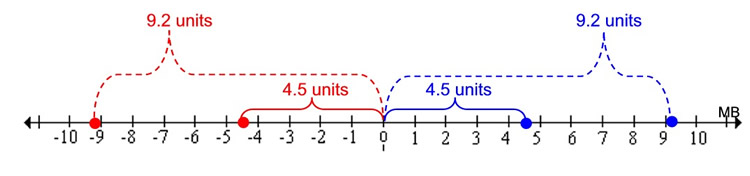
The difference between 9.2 and the opposite of 4.5 (which is -4.5) is 13.7.
Absolute value can be used to find this number line distance.
The distance between values a and b is | a - b | or | b - a |.
In this problem, we have | 9.2 - -4.5 | = | 13.7 | = 13.7,
or we could have | -4.5 - 9.2 | = | -13.7 | = 13.7.

 Ordering Rational Numbers: Ordering Rational Numbers:
The process of ordering rational numbers is the same as that of integer values. You are comparing numbers to determine which value is larger. Plot both values on a number line and see which value is farthest to the right. That will be the larger of the two values.
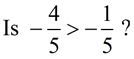
The answer is NO. On the number line we can see that
-1/5 is farther to the right, making it the larger value. |
 |
Because rational numbers can be written in several different forms, it can sometimes be challenging to determine the order of the numbers.
 Order the following list of rational numbers from least to greatest. Order the following list of rational numbers from least to greatest.
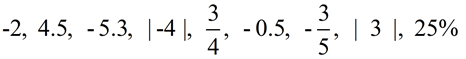
It will be difficult to decide upon a scale for a number line, since this list of numbers is a combination of integers, fractions, decimals and percents. It will be easier in this situation to convert the numbers to one "form" to determine the order.
The easiest way to order rational numbers,
is to covert them all to decimals. |
 Absolute value is a distance from zero on a number line and is always positive (or zero). Absolute value is a distance from zero on a number line and is always positive (or zero).
Replace the absolute value quantities with their equivalence.

 To change a fraction to a decimal, divide the numerator by the denominator. To change a fraction to a decimal, divide the numerator by the denominator.
Convert the fractions to decimals.

 To change a percent to a decimal, move the decimal point two places to the left. To change a percent to a decimal, move the decimal point two places to the left.
Convert % to decimal.
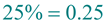
Substitute the equivalent expressions into the original problem.
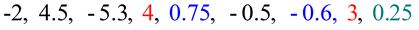
 Negative numbers are always less than positive numbers. Negative numbers are always less than positive numbers.
Push the negative values to the left, and push the positive values to the right.

 Arrange the negative numbers in order, and then the positive numbers in order, from least to greatest. Arrange the negative numbers in order, and then the positive numbers in order, from least to greatest.
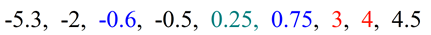
 Convert back to original listings. Convert back to original listings.
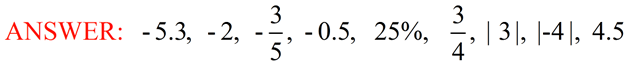
 Now that we know how these numbers are "related" to one another (in their decimal forms), let's put them on a number line. The number line is not required in the answer to this question. Now that we know how these numbers are "related" to one another (in their decimal forms), let's put them on a number line. The number line is not required in the answer to this question.

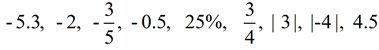
|