When working with numerical or algebraic expressions containing two or more operations, there is a conventional order in which operations are performed. If an ordering precedence did not exist, operations could potentially yield more than one correct answer.
Does 9 - 3 x 2 = 3 ? |
OR |
Does 9 - 3 x 2 = 12 ?
|
This one is correct! |
|
This one is NOT correct! |
|
You need to know and remember this ordering:
 Order of Operations: Proceed in this order: Order of Operations: Proceed in this order: |
| |
1. Parentheses are done first
2. Exponents are done next
3. Multiplication and Division (done as they are encountered left to right)
4. Addition and Subtraction (done as they are encountered left to right) |
|
An acronym that is used to help remember this order is PEMDAS.
Parentheses, Exponents, (Multiplication/Division), (Add/Subtract).
Common Mnemonic Phrase: "Please Excuse My Dear Aunt Sally".
There are also other phrases that can be used, or you can make up your own. |
 |
|
While PEMDAS lists M before D, remember that multiplication and division are done as they are read from left to right. It may not always be the case that multiplication is done "before" division.
The expression 16 ÷ 4 x 2 = 8 (not 2).
The same is true of addition and subtraction: 8 - 4 + 2 = 6 (not 2). |
|
You will need to follow "order of operations" when working with a variety of mathematical topics: evaluating formulas, solving equations, evaluating algebraic expressions, and simplifying monomials and polynomials. Let's look at simplifying some numerical expressions.
|
Simplify 6 + 5 x 4 |
|
6 + 20 |
|
Multiply |
26 |
|
Add |
|
Simplify 8 + ½ x 12 + 15 ÷ 5 |
|
8 + 6 + 15 ÷ 5 |
|
Multiply |
8 + 6 + 3 |
|
Divide |
17 |
|
Add |
|
Simplify 3(8 + 1) - 4(8 - 5) |
|
3(9) - 4(3) |
|
Parentheses |
27 - 12 |
|
Multiply |
15 |
|
Subtract |
 |
When working with a fraction bar (the bar meaning "division"), it is implied that a set of parentheses surrounds everything in the numerator (top) and a set of parentheses surrounds everything in the denominator (bottom).
Simplify the top, simplify the bottom, then deal with the fraction bar.
Consider the example below as if it was written (62 + 5 - 32) / (8 - 4).
|
|
|
Simplify 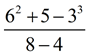
|
|
|
|
Exponents (top) |
|
|
Add/Subtract (top); Subtract (bottom) |
8 |
|
Divide (fraction bar = divide) |
|
Simplify 23 + (3 + 2)(6 - 3) |
|
23 + (5)(3) |
|
Parentheses |
8 + (5)(3) |
|
Exponent |
8 + 15 |
|
Multiply |
23 |
|
Add |

Now, let's try a couple of more challenging situations:
|
Simplify 30 - (8 - 15 ÷ 3) x 2 |
|
30 - (8 - 5) x 2 |
|
Parentheses; Divide first |
30 - (3) x 2 |
|
Parentheses; Subtract |
30 - 6 |
|
Multiply |
24 |
|
Subtract |
|
Simplify 2(20 - 32 + 1) - (42 ÷ 2 x 3) |
|
2(20 - 9 + 1) - (42 ÷ 2 x 3) |
|
Parentheses; Exponent |
2(20 - 9 + 1) - (21 x 3) |
|
Parentheses; Divide |
2(12) - (21 x 3) |
|
Parentheses; Subtract; Add |
2(12) - (63) |
|
Parentheses; Multiply |
24 - (63) |
|
Multiply |
-39 |
|
Subtract |
|