A proportion is an equation that states
that two ratios are equal, such as
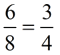 |
|
|
A proportion can be written in two ways:
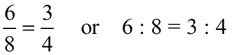
Both are read "6 is to 8 as 3 is to 4".
In a proportion the first and last terms (6 and 4) are called the extremes.
The second and third terms (8 and 3) are called the means.
|
|
Determine if a Proportion is TRUE:
You can tell if a simple proportion is true by looking at each of the ratios (fractions). If the fractions both reduce to the same value, the proportion is true. The fractions are equivalent. |
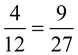 A TRUE proportion:
A TRUE proportion:
both fractions reduce to 1/3. |
| Find a Missing Part (a Variable) in a Proportion: |
 Simple Approach: Simple Approach:
Remember that both fractions in a proportion must represent the same value. We can solve for a missing part of a proportion (the variable) by finding a common denominator for the two fractions. This will let you find the missing part.
While useful, this approach may not be sufficient when working with more complicated proportions.
|
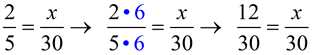 To find x, use the common denominator of 30.
To find x, use the common denominator of 30.
To change 5 to 30, multiply by 6.
The SAME must be done to the top,
(multiply 2 by 6) to keep the fractions equal.
ANSWER: x = 12 |
 Universal Rule: Universal Rule:
There is a rule (or algorithm) that can be followed to determine if two fractions are equal. The process multiplies from the top "across" to the bottom between the fractions in the proportion. If these products are equal, the fractions are equal. This method is very handy for setting up an equation to solve for a variable.
A precise statement of the rule is:
RULE: In a true proportion, the product of the means equals the product of the extremes. |
|
|
|
Solve for x: |
|
Using
RULE: |
5 (x) = (2)(30)
5x = 60
x = 12 |
|
Cross Multiplication Algorithm (Rule):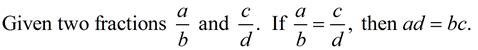
|
|
An algorithm is a process or set of rules to be followed in calculations or problem solving. |
|
Does this rule really work? Let's take a closer look at what is happening.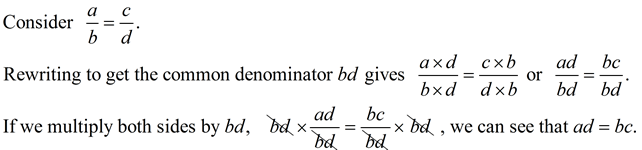
This algorithm is simply the result of rewriting fractions to have the same denominator, and then examining their numerators. |
Tidbit of Info: A proportion can be rewritten in different ways, yet remain true.
The following proportions are all equivalent (mathematically the same).
Check that this is true using "cross multiply".
|
By Cross Multiply, all of these proportions can create
10y = 5x. |
|

Method 1:
Perhaps you notice that each of these
ratios (fractions) can be simplified to 1/3,
which
indicates that the proportion is TRUE. |
Method 2: (using RULE)
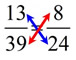 (13)(24) = (39)(8) (13)(24) = (39)(8)
312 = 312 (TRUE)
|
|
Method 1:
Getting a common denominator: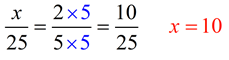 |
Method 2: (using RULE)
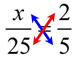 |
(x)(5) = (25)(2)
5x = 50
x = 10 |
|
|
Method 1:
Getting a common denominator is not as easy in
this problem as it was in Example 2. The common denominator will be 11x (where x represents the empty box). You can, in this problem, notice that
8 x 4 = 32. Multiplying the denominator by this same value will create a TRUE proportion: 11 x 4 gives the answer 44.
If you want to use 11x as the common denominator,
you will get:
|
|
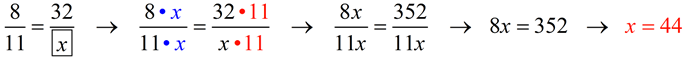 |
|
 |
The ratio of boys to girls in Spanish club is 4 to 5. If there are 25 girls in the club, how many boys are in the club? |
Method 1:
Use the common denominator of 25:
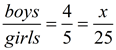 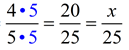
x = 20 means there are 20 boys in the club. |
Method 2:
Using the rule:
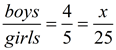
4•25 = 5•x
100 = 5x
x = 20 means there are 20 boys in the club. |
|
 |
When setting up a proportion in a word problem, it is important to remember to keep the same "units" in both numerators, and the same "units" in both denominators.
Such as:
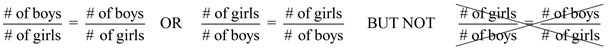
|
|
 |
The length of a stadium is 100 yards and its width is 75 yards. If 1 inch represents 25 yards, what would be the dimensions of the stadium drawn on a sheet of paper? |
Method 1:
This problem can be solved by an intuitive approach, such as:
100 yards by 75 yards
100 yards = 4 inches (HINT: 100/25 created the 4)
75 yards = 3 inches (HINT: 75/25 created the 3)
Therefore, the dimensions would be 4 inches by 3 inches. |
Method 2:
In the following proportions, notice that the inches are all on the top and the yards are all on the bottom for this solution. Other setups are possible.
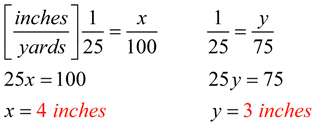 |
|
|