To create a number line representation of a fraction:
1. Draw a number line.
2. Label the location of 0 and 1 (leave plenty of room) |
|
3. The denominator (bottom) will tell you the number of equal sections to create
between 0 and 1.
4. The numerator (top) will tell you the number of the equal sections to shade to
represent the fraction. |

 Decomposing Fractions: (breaking fractions down into parts)
Decomposing Fractions: (breaking fractions down into parts)
A single fraction can be represented as several fractions put together (added together).
All of these entries represent the same quantity, which is 7 "one-eighth" sections, as seen by the same total shadings in the diagrams. In the second and third listings above, notice that the numerators add up to the numerator of the original (first) fraction which is 7.
 Improper Fractions and Mixed Numbers:
Improper Fractions and Mixed Numbers:
A proper fraction is a fraction that is less than one, with the numerator (top) less than the denominator (bottom). It is the type of fraction we most often see, such as ¼, ¾, and ½.
An improper fraction is a fraction where the numerator (top) is greater than (or equal to) the denominator (bottom).
The fraction 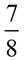 can be thought of as 7 x
can be thought of as 7 x 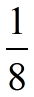 , described as "7 one-eighths", and displayed as:
, described as "7 one-eighths", and displayed as:
The fraction
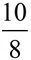 can be thought of as 10 x
can be thought of as 10 x 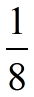 , described as "10 one-eighths", and displayed as:
, described as "10 one-eighths", and displayed as:
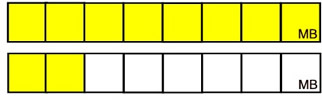
Notice that in the improper fraction we have the entire "whole" plus a little more. Improper fractions may have ONE copy of the "whole" or multiple copies of the "whole".
Notice in this problem we have "ONE whole" plus "2 one-eighths".
This can be written as a mixed number as 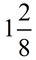 . We now know that
. We now know that 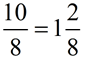 .
.
A mixed number is number consisting of an integer and a proper fraction.
Improper fractions can be changed into mixed numbers, as we saw above.
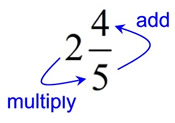
A quick method to covert a mixed number to an improper fraction:
Convert 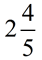 to an improper fraction. to an improper fraction.
Multiply the whole times the denominator,
and
add the numerator.
2 x 5 + 4 = 14
This number will be the numerator
of the improper fraction.
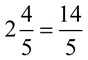
|
 2 x 5 + 4 = 14
2 x 5 + 4 = 14 |
|
|
 |
When dealing with mixed numbers, remember what you say when you read the number aloud. 4½ is read as "4 and one-half"
The "and" means addition, not multiplication.
4½ = 4 + ½ 4½ ≠ 4 x ½
|
|

NOTE:
|
In mathematics, the word fraction is also used to describe mathematical expressions that are not rational numbers (where the numerator and denominator are not integers).
For example, there are expressions that contain radicals such as 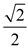 , and expressions such as 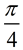 that are referred to as fractions.
There are also algebraic fractions such as 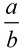 where the values of a and b are not known (assuming b ≠0).
|
|
|
For help with fractions
on your calculator,
click here. |
|