 |
Rules for Adding fractions:
1. The bottom numbers (denominators) must be the same.
2. Add the top numbers (numerators)
Put this answer over the denominator.
3. Simplify the fraction, if possible.
Remember: "common denominators"
("common denominators" means the "same" denominators) |
Same Denominators:
"Common Denominators" |
|
When the fractions have the same denominators, addition and subtraction are easy.
|
When adding (or subtracting) fractions with the same denominators,
just add (or subtract) the numerators.

|
When fractions have different denominators, you must find a common denominator.
|
When adding (or subtracting) fractions with different denominators,
you must find a common denominator before adding (or subtracting).
When you are looking for the least common denominator, you are looking for the smallest number that both denominators will divide into exactly.
 Remember, you can always multiply the two denominators together to get a common denominator. This number may not be the "least" common denominator, but it will do the job. Remember, you can always multiply the two denominators together to get a common denominator. This number may not be the "least" common denominator, but it will do the job.
Adding fractions depends upon whether a common denominator is present.
The Fundamental Law of Fractions (applied to adding fractions) discusses this
need of a common denominator.
Fundamental Law of Fractions (applied to adding fractions):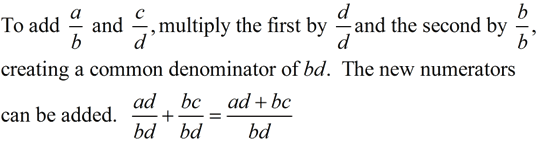 (Note: bd will not necessarily be the "least" common denominator)
(Note: bd will not necessarily be the "least" common denominator) |
In plain English, this law is telling us that we can find a common denominator by finding the product (the multiplication) of the two existing denominators. The numerators must then be adjusted accordingly.
(bd is the product of the two denominators)

Adding Fractions on the Number Line: |
We are going to be looking at the addition of fractions using number lines.
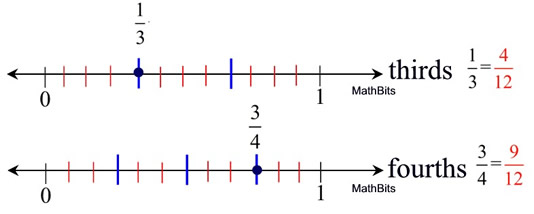
When 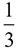 and and 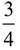 are plotted on number lines, the subdivisions (sections) on the number lines are different. One of the subdivision is "thirds" and the other is "fourths". Because of this difference in the size of these sections, we have no way of combining (or adding) them together. It would be like adding apples and dogs and wondering what you actually had when you were done. An "appledoodle", maybe???? Smile! are plotted on number lines, the subdivisions (sections) on the number lines are different. One of the subdivision is "thirds" and the other is "fourths". Because of this difference in the size of these sections, we have no way of combining (or adding) them together. It would be like adding apples and dogs and wondering what you actually had when you were done. An "appledoodle", maybe???? Smile!
There must be a way to "fix" the subdivisions (sections) so that they could be the same size. The trick is to make more equal subdivisions until we have the same equal number on each line.
.(Finding the needed number of subdivisions, will create our common denominator.)
On the "thirds" line, if we cut each "third" into four equal sections we will get 12 in total.
On the "fourths" line, if we cut each "fourth" into three equal sections we will get 12 in total.
(This number 12 will be called our common denominator.)
Add:
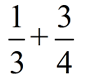 |
|
Now that both lines contain subdivisions of the same size (both have 12 sections), we can express our fractions using this new subdivision size of 1/12. Then we can add the fractions together (since they are representatives of the same size sections). Now we are adding apples to apples.
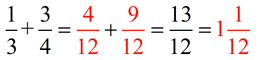
Let's combine our number lines onto one line to demonstrate this sum.
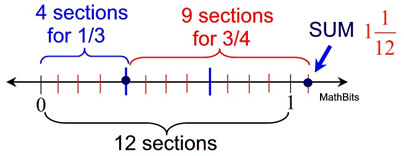
Notice that the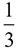 , when multiplied top and bottom by 4, creates our new fraction , when multiplied top and bottom by 4, creates our new fraction  . .
(4 was the number of subdivisions we created for each "third" section)
Notice that the 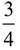 , when multiplied top and bottom by 3, creates our new fraction , when multiplied top and bottom by 3, creates our new fraction 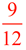 . .
(3 was the number of subdivisions we created for each "fourth" section)

|
For help with fractions
on your calculator,
click here. |
|
|