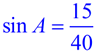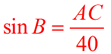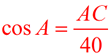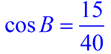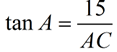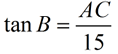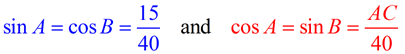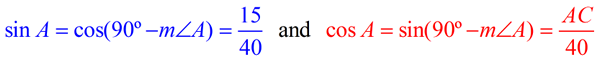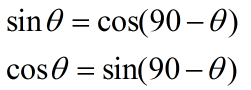|
 |
The sine of any acute angle is equal to the cosine of its complement. |
|
Let's start our investigation of this concept by looking at an example:
In right triangle ACB, as shown below, m∠A = 22º, BC = 15 and AB = 40. Express the ratios of sine, cosine and tangent for both ∠A and ∠B.
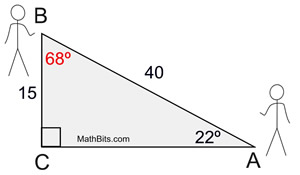
Since m∠A = 22º is given, we know m∠B = 68º since there are 180º in the triangle. Notice that ∠A and ∠B are complementary (they add to 90º).
|
From
reference
angle A (22º) |
From reference
angle B (68º) |
|
|
|
|
|
|
When you list the trigonometric ratios for both acute angles in a right triangle, you notice some interesting developments.
Let's concentrate on sine and cosine: |
Observation from the table above: 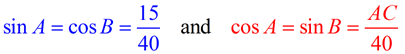
In a right triangle, the sine of one acute angle, A, equals the cosine of the other acute angle, B.
If ∠A and ∠B are the acute angles of a right triangle,
sin A = cos B |
Since the measures of these acute angles of a right triangle add to 90º,
we know these acute angles are complementary. ∠A is the complement of ∠B, and ∠B is the complement of ∠A.
If we write, m∠B = 90º - m∠A (or m∠A = 90º - m∠B ), and we substitute into the original observation, we have:
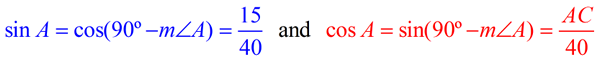
If θ is substituted for m∠A , we establish the following relationship between sine and cosine:
The sine of any acute angle is equal to the cosine of its complement.
The cosine of any acute angle is equal to the sine of its complement.
Sine and cosine are called "cofunctions", where the sine (or cosine) function
of any acute angle
equals its cofunction of the angle's complement.

Yes, there is a "relationship" regarding the tangent of the two acute angles (A and B) in a right triangle. It is not, however, the same type of relationship that exists between sine and cosine.
The tangent of
∠A is the reciprocal (flip over) of the tangent of ∠B.

The angles being used in the following examples are acute angles.
If sin 30º = ½ and cos θ = ½,
find
θ. |
Solution: Since both trig functions = ½,
30º and θ must be complementary.
θ = 60º
|
If sin(3x + 10)º = cos(x + 24)º,
find x. |
Solution: In order for the sine and cosine to be equal, the angles must be complementary.
3x + 10 + x + 24 = 90
4x + 34 = 90
4x = 56
x = 14 |
If sin(15º) = 0.26 and
cos (15º) = 0.97,
find sin(75º) and the cos(75º). |
Solution: The sine of an angle and the cosine of its complement are equal.
15º and 75º are complementary.
sin(75º) = cos(15º) = 0.97
cos(75º) = sin(15º) = 0.26 |
In right ΔABC, m∠C = 90º,
sin A =
x + 0.1 and cos B = 2x - 0.4. Find x. |
Solution: If A and B are the acute angles of a right triangle, sin A = cos B.
x + 0.1 = 2x - 0.4
0.5 = x
|

 Trigonometric Functions on the TI-84+ Calculator Trigonometric Functions on the TI-84+ Calculator |
Remember to set your graphing calculator to
DEGREE MODE. |
|
For help with
trig ratios on
your calculator,
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|