|
Directions: Carry the full calculator value until rounding the final answer.
1. |
Cody is building a dog house for his dog, Fido. The house is 3 ft. wide, 3 ft. tall, and 4 ft. deep, and the roof makes a 58º angle with the horizontal. The special shingles for the roof come in 9 sq. ft. bundles at $15.95 per bundle. Find the price of shingling the roof when the shingles must be purchased in complete bundles. Express answer to nearest penny.
Choose:
|
|
|
2. |
Alex is standing in the hay loft doorway of the barn looking at a nearby tree. The horizontal distance from Alex to the tree (A) is 30 feet. The angle of elevation of a bird (B) at the top of the tree is 32º and the angle of depression of his dog (C) at the foot of the tree is 40º. What is the height of the tree, to the nearest tenth of a foot ? |
| |
|
| |
Choose:
|
|
|
3. |
From the top of the Eiffel Tower, a jogger is spotted heading toward the tower. At 2 pm, the angle of depression of the jogger (A) was measured to be 37º. Four minutes later, (B), when measured again, the angle of depression had increased by 35º. Find the average speed of the jogger to the nearest foot per minute. |
| |
|
| |
Choose:
|
|
|
4. |
A spaceship beams a robot to the Earth's surface. The robot travels approximately 3,500 meters at an angle of depression of 68.5º from the ship down to the surface. During the beaming, the robot's vertical rate of descent is 1000 meters per second. How long did it take the robot to land on the surface, to the nearest hundredth of a second ?
|
|
| |
Choose:
|
|
|
5. |
Rabbit A and rabbit B are sitting 36 feet apart. Between them is their home (rabbit hole C) beneath a bamboo tree. From point A, the angle of elevation of the top of the tree is 52º, and from point B the angle of elevation of the top of the tree is 48º. Find, to the nearest tenth of a foot, the height of the tree.
|
| |
|
| |
Choose:
|
|
|
6. |
A camera is set to record a bungee jump from point B on the bridge. The end, A, of the vertical dormant cord (before stretching) is recorded as a 56º angle of depression from the camera. The horizontal distance from the camera to the secured cord, CB, is 34 feet. The vertical distance from the top of the rail to the water is 96 feet.
|
|
| |
a) Find the dormant length of the bungee cord, BA, to the nearest tenth of a foot.
Choose:
|
| |
b) The bungee cord's maximum stretch is 80% of its dormant length. Find the length of the cord when it is fully stretched, to the nearest tenth of a foot.
Choose:
|
| |
c) Find the camera's angle of depression needed to record the end of the bungee cord when stretched to its maximum length. (Round angle to the nearest tenth of a degree.)
Choose:
|
| |
d) The person jumping is 6 feet tall. Describe the situation, in relation to the water, when the cord is stretched to its maximum length.
|
| |
|
|
7. |
While fighting a forest fire, several firemen are trapped behind the burn line of the fire. A rescue plane is searching for the firemen.
|
| |
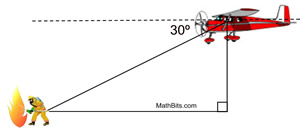
a) Cruising at 1500 feet, the plane spots one of the firemen ahead on the ground at an angle of depression of 30 degrees. What is the plane's horizontal distance, to the nearest foot, from the fire fighter?
Choose:
|
|
| |
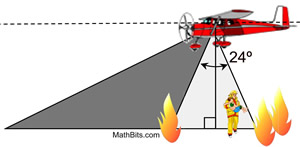
b) As night falls, the rescue plane continues cruising at 1500 feet to search for the missing firemen using a spotlight. |
| |
The view of the spotlight is 24º, as shown in the diagram. What is the width of the ground covered by the spotlight, to the nearest foot.
Choose:
|
|
|
8. |
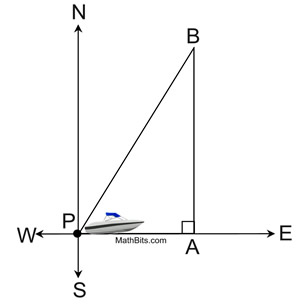
A boat travels at 20 kph due east for one and one-half hours from point P to point A. It then travels due north, at the same speed, for three and one-half hours to point B.
|
| |
a) If the boat had originally traveled directly from point P to point B, what would be the distance traveled, to the nearest kilometer?
Choose:
|
 |
| |
b) What is the angle, from true North, that the boat will be traveling from point P to point B, to the nearest degree?
Choose:
|
| |
|
|
9. |
Given: In isosceles ΔABC, the base BC = 20 units and the vertex ∠BAC = 38º.
|
| |
a) Find the length of altitude 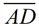 to the nearest unit. to the nearest unit.
Choose:
b) Using the answer from part a, find the area of ΔABC.
Choose:
|
|
| |
c) Using the answer from part b, find the length of altitude 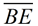 to side to side 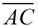 , to the nearest tenth of a unit. , to the nearest tenth of a unit.
Choose: |
| |
|
|
10. |
A car travels along an inclined road, in the desert, at 55 mph for 6 hours, from point A to point B.
|
| |
a) If the horizontal distance of this section of the road is 327 miles, what is the angle of elevation of the road to the nearest hundredth of a degree?
|
|
| |
|
| |
b) Using the answer from part a, find the vertical distance (height) of the road, BC, to the nearest hundredth of a mile.
Choose:
|
| |
c) Engineers want to raise the incline of this section of the road by increasing the vertical distance by 12 miles. What will be the new angle of elevation of the road, to the nearest tenth of a degree?
Choose:
|
| |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|