|
Navigation is a field of study that focuses on monitoring the movement of vehicles from one location to another. The term "bearing" is used when dealing with navigation, and may take on varying definitions depending upon its context.
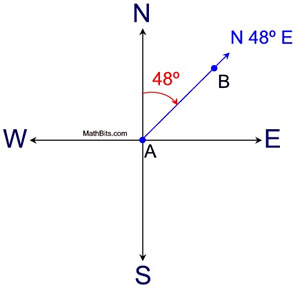
 The US Army defines the bearing from point A to point B as the angle between a north (or south) ray with origin at A, and the ray starting at A and containing point B. The US Army defines the bearing from point A to point B as the angle between a north (or south) ray with origin at A, and the ray starting at A and containing point B. A bearing consists of 2 characters and one number, such as N 48º E.
This is a very popular method for determining position as it is easily understood. Three additional examples:
|
 |

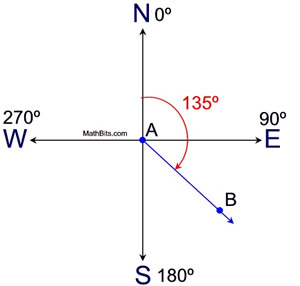
 Airplane pilots define bearing as an angle measured clockwise from North. For example, East is 90º, South is 180º, South-West is 225º and so on.
The diagram at the right shows an airplane flying at a bearing of 135º. Airplane pilots define bearing as an angle measured clockwise from North. For example, East is 90º, South is 180º, South-West is 225º and so on.
The diagram at the right shows an airplane flying at a bearing of 135º.
When a problem involves the word "bearing", the manner in which the angle is presented will tell you which of these two methods is being used. Both methods may appear in problems relating to the Law of Sines or the Law of Cosines.
See the navigation example problem at the bottom of this page. |
 |

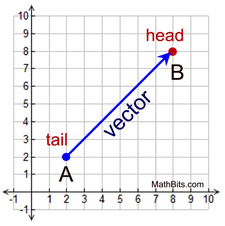
A vector is a quantity that has magnitude (length) and direction.
A vector is represented by a directed line segment, which is a segment with an arrow at one end indicating the direction of movement. Unlike a geometric ray, a directed line segment has a specific length.
In relation to the Law of Sines and Law of Cosines, problems will refer to the "resultant vector". The resultant vector is the "result" of adding two (or more) vectors.
There are two common methods of finding resultant vectors. |
 |
Method 1: (Head to tail method)
In this method, the tail of one vector is "slid up" (translated) to attach to the head of the other vector.
The second diagram shows how this new position will set up for an application of the Law of Cosines.
|
Given two vectors representing forces acting upon one object, separated by 35º. Find the resultant vector.
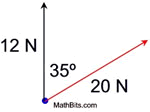 |
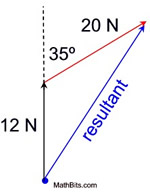
("N" stands for "newtons",
a unit of force.) |
One newton is the force needed to accelerate 1 kilogram of mass at the rate of 1meter per second squared.
Method 2: (Parallelogram method)
In this method, the original diagram is used to create a parallelogram. The opposite sides of the parallelogram are congruent and the consecutive angles are supplementary. The resultant vector is the diagonal of the parallelogram. |
Given two vectors representing forces acting upon one object, separated by 35º. Find the resultant vector.
 |
|
You can see that both of these methods create the same situation. The Law of Cosines (or the Law of Sines depending upon the problem) will be valuable in solving these problems.
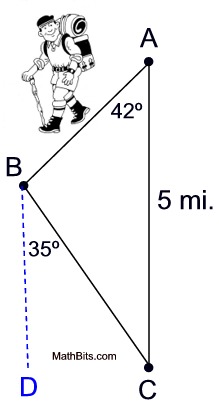
A hiker starts at point A and travels in a direction S 42º W to point B, then S 35º E to point C which is directly south of A, and finally returns 5 miles directly to point A. Find the total distance hiked, to the nearest tenth of a mile.
Solution:
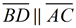 since both represent a north-south direction. Alternate interior angles ∠DBC and ∠BCA are congruent. since both represent a north-south direction. Alternate interior angles ∠DBC and ∠BCA are congruent.
m∠ABC = 103º. Since we are dealing with two angles and two sides, the Law of Sines will apply.
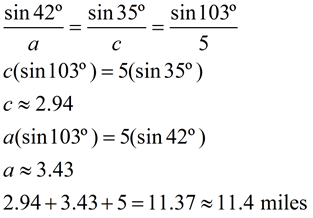 |
Answer: 11.4 miles
|
Two forces with magnitudes of 20 newtons and 12 newtons and an angle of 35º between them are applied to an object. Find the magnitude of the resultant vector to the nearest whole number.
Solution:
Using the parallelogram method, create a parallelogram with opposite sides parallel and opposite sides equal in measure. The consecutive angles of a parallelogram are supplementary, so m∠ABD = 145º. BD = 20 N. The magnitude of the resultant will be the length of the diagonal from A to D. Since we are dealing with one angle and three sides, the Law of Cosines applies.
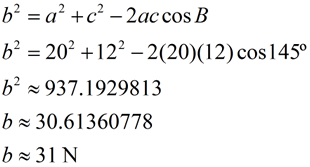 Answer: 31 N Answer: 31 N |

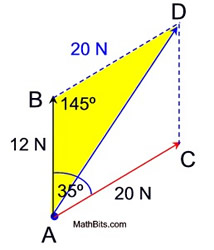
For the Law of Cosines formula,
let b = AD; a = BD and c = BA.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|






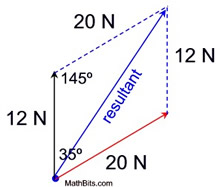
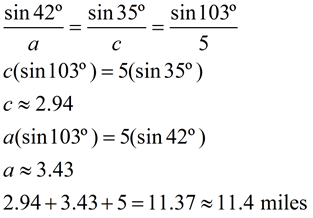

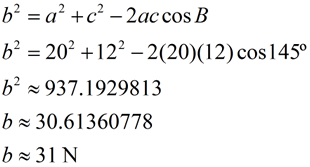 Answer: 31 N
Answer: 31 N