|
A rotation is a transformation that turns a figure about a fixed point called the center of rotation.
• An object and its rotation are the same shape and size, but the figures may be turned in different directions.
• Rotations may be clockwise or counterclockwise.
When working in the coordinate plane:
• assume the center of rotation to be the origin unless told otherwise.
• assume a positive angle of rotation turns the figure counterclockwise, and a negative angle turns the figure clockwise (unless told otherwise). |
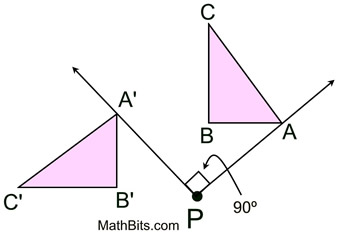 The triangle is rotated about P. The letters used to label
The triangle is rotated about P. The letters used to label
the triangle have not been rotated. |
Rotations can be seen, in a variety of situations:
The Earth |
Windmills |
Pinwheel |
The Earth experiences one complete rotation on its axis every 24 hours.
 |
The blades on windmills convert the energy of wind into rotational energy.
 |
A children's toy that rotates when blown.

|
Amusement Park Swing |
Ferris Wheel |
Merry-Go-Round |
Amusement park rides, such as the swing, allow you to become part of a rotation. |
Ferris wheels rotate about a center hub. (Yes, the seats tilt to prevent falling.)  |
On the merry-go-round, riders become part of the rotation about the center of the ride.

|
Rotations centered at the origin:
|
(x,y) becomes (-y,x) |
Rotation of 180º: |
(x,y) becomes (-x,-y) |
Rotation of 270º: |
(x,y) becomes (y,-x) |
|
Rotations in the coordinate plane are counterclockwise.
Remember: |
Clockwise:  |
Counterclockwise:
 |
|
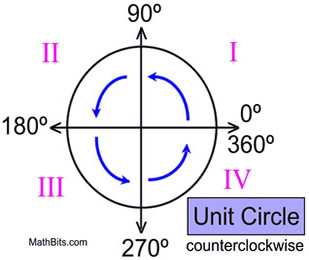
When working with rotations, you should be able to recognize angles of certain sizes. Popular angles include 30º (one third of a right angle), 45º (half of a right angle), 90º (a right angle), 180º, 270º and 360º.
You should also understand the directionality of a unit circle (a circle with a radius length of 1 unit). Notice that the degree movement on a unit circle goes in a counterclockwise direction, the same direction as the numbering of the quadrants: I, II, III, IV. Keep this picture in mind when working with rotations on a coordinate grid. |
 |
Rotations in the coordinate plane:
Keep in mind that rotations on a coordinate grid are considered to be counterclockwise, unless otherwise stated. While most rotations will be centered at the origin, the center of rotation will be indicated in the problem (or in the notation).
 Rotation 90º:
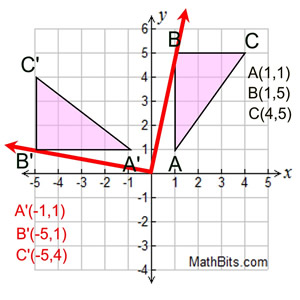 |
Starting with ΔABC, draw the rotation of 90º centered at the origin. (The rotation is counterclockwise.)
To "see" that this is a rotation of 90º, imagine point B attached to the red arrow. The red arrow is then moved 90º (notice the 90º angle formed by the two red arrows). Look at the new position of point B, labeled B'. This same approach can be used for all three vertices.
Rotation of 90º on coordinate axes.
Centered at origin.
(x, y) → (-y, x) |
|
 Rotation 180º:
 |
Starting with ΔABC, draw the rotation of 180º centered at the origin. (The rotation is counterclockwise.)
As we did in the previous example, imagine point B attached to the red arrow from the center (0,0). The arrow is then moved 180º (which forms a straight line). Notice the new position of B, labeled B'.
Rotation of 180º on coordinate axes.
Centered at origin.
(x, y) → (-x, -y)
(same as point reflection in origin) |
|
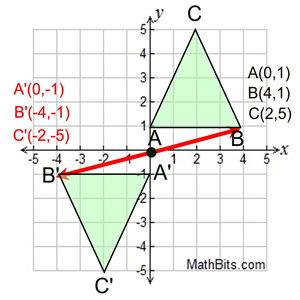
 Rotation 270º:
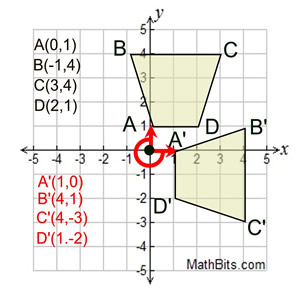 |
Starting with quadrilateral ABCD, draw the rotation of 270º centered at the origin. (The rotation is counterclockwise.)
As we did in the previous examples, imagine point A attached to the red arrow from the center (0,0). The arrow is then moved 270º (counterclockwise). Notice the new position of A, labeled A'. Since A was "on" the axis, A' is also on the axis.
Rotation of 270º on coordinate axes.
Centered at origin.
(x, y) → (y, -x ) |
|

 |
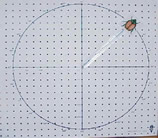
If the rotation angles are giving you trouble, imagine a unit circle with a movable "bug" on a radial arm from the origin. Swing the "bug" around and look at the angle created by the move, and the position of the "bug".
|
 |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
