|
 |
Reflections are FLIPS!! |
|
A reflection can be thought of as folding or "flipping" an object over the line of reflection.
• The original object is called the pre-image, and the reflection is called the image.
• The image is usually labeled using a prime symbol, such as A'B'C'.
• An object and its reflection have the same shape and size, but the figures face in opposite directions. The objects appear as if they are mirror reflections, with right and left reversed. These triangles are congruent.
|
 |
A reflection can be seen, for example, in water, a mirror, or in a shiny surface. Take a look at the following reflections.
Reflection in Water |
Reflection in a Mirror |
Reflection in Shiny Surface |
|
|
|
Reflections in the coordinate plane:
 Reflect over the x-axis: Reflect over the x-axis: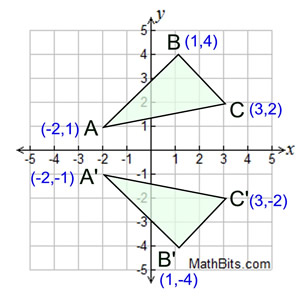
|
When you reflect a point across the x-axis, the x-coordinate remains the same, but the y-coordinate is transformed into its opposite (its sign is changed).
If you forget the rules for reflections when graphing, simply fold your paper along the x-axis (the line of reflection) to see where the new figure will be located.
Or you can measure how far your points are away from the x-axis to locate the new points, such as B is 4 vertical units above the x-axis, so B' will be 4 vertical units below the x-axis.
The reflection of the point (x,y) across
the x-axis is the point (x,-y).
|
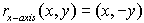 |
 Reflect over the y-axis: Reflect over the y-axis: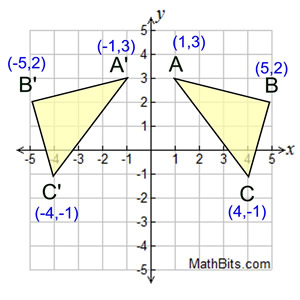 |
When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed).
Notice that B is 5 horizontal units to the right of the y-axis, and B' is 5 horizontal units to the left of the y-axis.
The reflection of the point (x,y) across
the y-axis is the point (-x,y).
|
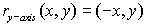 |
 Reflect over y = x: 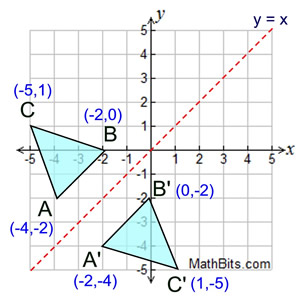 |
When you reflect a point across the line y = x, the x-coordinate and y-coordinate change places. If you reflect over the line
y = -x, the x-coordinate and y-coordinate change places and are negated (the signs are changed).
The reflection of the point (x,y) across
the line y = x is the point (y, x).
|
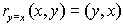
The reflection of the point (x,y) across
the line y = -x is the point (-y, -x). |
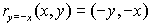 |
 Reflect over any line: 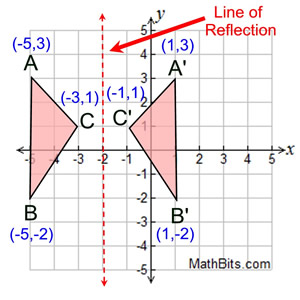 |
Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure. The line of reflection will lie directly in the middle between the original figure and its image.
The line of reflection is the perpendicular bisector of the segment joining any point to its image.
Notice that each point of the original figure and its image are the same distance away from the line of reflection. You may be able to simply "count" these distances on the grid. |
|
A small plastic device, called a Mira™ , can be used when working with line reflections. The Mira is placed on the line of reflection and the original object is reflected in the plastic. By looking through the plastic, you can see what the reflection will look like on the other side and you can trace it with your pencil.
|

|

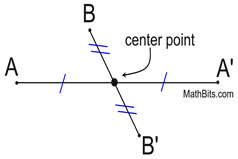
Reflection in a Point:
A point reflection (or point symmetry) exists when a figure is built around a single point called the center of the figure, or point of reflection. For every point in the figure, there is another point found directly opposite it on the other side of the center such that the point of reflection becomes the midpoint of the segment joining the point with its image. Under a point reflection, figures do not change size or shape. |
 |
While any point in the coordinate plane may be used as a point of reflection, the most commonly used point is the origin. Assume that the origin is the point of reflection unless told otherwise.
 Reflect in origin (0,0): 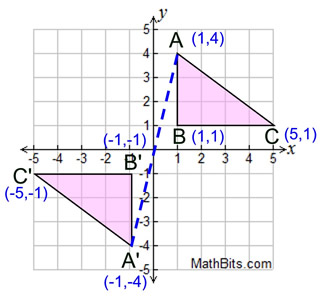 |
Triangle A'B'C' is the image of triangle ABC after a point reflection in the origin.
Imagine a straight line connecting A to A' where the origin is the midpoint of the segment.
When you reflect a point in the origin, both the x-coordinate and the y-coordinate are negated (their signs are changed).
In a point reflection in the origin, the image of the point (x,y) is the point (-x,-y). |
|
A point reflection creates a figure that is congruent to the original figure.
As a rigid transformation, a point reflection preserves length.
Since the orientation in a point reflection remains the same
(such as counterclockwise seen in this diagram),
a point reflection is more specifically called a direct rigid transformation.


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|













