|

also called an isometry |
A rigid transformation is a transformation in the plane that preserves distance (length) between every pair of points. As such, angle measure is also preserved. Basically, the size and shape of the figure do not change. |
|
Reflections, translations, rotations,
and combinations of these three transformations,
are "rigid transformations".
Side
Note: |
You may see the term "Rigid Motion" used to refer to "Rigid Transformation". Be aware that there is also another meaning of "Rigid Motion". "Rigid Motion" can also be defined and interpreted as only translations and rotations, eliminating reflections as they do not perserve orientation. [WolframAlpha] |

While the pre-image and the image under a rigid transformation will be congruent,
they may not necessarily be facing in the same direction.
Not all transformations are "rigid" transformations.
In a dilation, for example, the object changes its size.
Dilations are NOT rigid transformations.

Let's look at some examples:
Rigid Transformations
Reflection over the y-axis: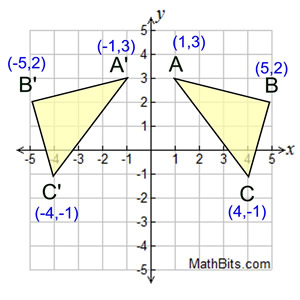 |
A reflection flips an object over an imaginary line in the center.
In this reflection, the imaginary line is the
the y-axis which is called the line of reflection (or the line of symmetry).
The reflection of the point (x,y) across
the y-axis is the point (-x,y).
(x,y) → (-x,y)
The corresponding sides of the triangles are of the same length.
The corresponding angles of the triangles are of the same measure.
The two triangles are congruent.
Rigid Transformation |
Translation 6 units left,3 units up:
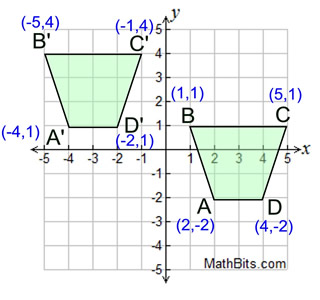 |
A translation slides (or pushes) an object.
The size and shape remain the same.
In this translation, trapezoid ABCD
moves 6 units to the left and 3 units up.
(x,y) → (x - 6, y + 3)
The corresponding sides of the trapezoids are of the same length.
The corresponding angles of the trapezoids are of the same measure.
The two trapezoids are congruent.
Rigid Transformation |
Rotation 90º about origin:
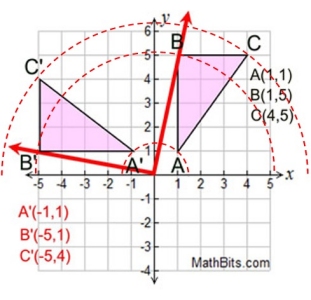 |
A rotation turns (or spins) an object about a point.
The size and shape remain the same.
In this rotation, ΔABC is rotated 90º counterclockwise about the origin.
(x,y) → (-y, x)
The corresponding sides of the triangles are of the same length.
The corresponding angles of the triangles are of the same measure.
The two triangles are congruent.
Rigid Transformation |
Non-Rigid Transformation
Dilation scale factor ½ at origin.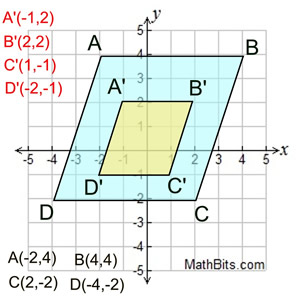 |
A dilation enlarges (reduces) an object centered from a specific point.
The size does NOT remain the same.
The shape does remain the same.
In this dilation, pre-image ABCD is decreased in size by a factor of ½.
(x,y) → (½x, ½y)
The corresponding sides of the quadrilaterals are NOT the same lengths.
BUT...
The corresponding angles of the quadrilaterals are of the same measure.
The two quadrilaterals are similar
(not congruent).
Non-Rigid Transformation |


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|