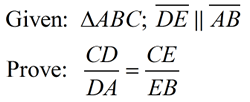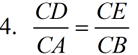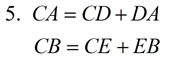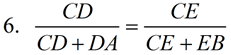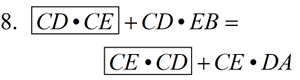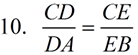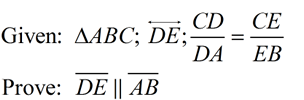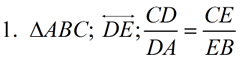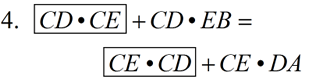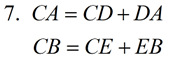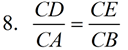|
In the previous lesson, we saw the Proportional Line Segment Theorem that stated that "three or more parallel lines intercept proportional segments on two or more transversals".
On this page, we will examine an application of that theorem associated with similar triangles.
The "Side Splitter" Theorem says that if a line intersects two sides of a triangle and is parallel to the third side of the triangle, it divides those two sides proportionally.

Find x.
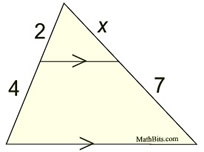 |
Apply the Side Splitter Theorem:
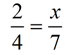 (form a proportion using the segment lengths) (form a proportion using the segment lengths)
Solve the proportion for x:
4x = (2)(7)
4x = 14
x = 3.5 (Answer) |
Notice in this example, that two of the four labeled "segments" are NOT sides of a triangle. This is an important observation when working with this theorem. |
In the diagram above, while the ratio of the segments shown is 2:4, or 1:2,
the ratio of the small triangle to the large triangle is NOT 1:2.
To find the ratio of the small triangle to the large triangle
requires using the FULL SIDES of each triangle, which gives 2:6 or 1:3.
In addition, once we know the ratio of the triangles' sides (1:3),
we also know the ratio of their areas is 1:9.
 NGMS Quote (pg.132): "When students use area as a device to establish results about proportions, such as the important theorem (Side-Splitter Theorem), they are making use of structure. NGMS Quote (pg.132): "When students use area as a device to establish results about proportions, such as the important theorem (Side-Splitter Theorem), they are making use of structure.

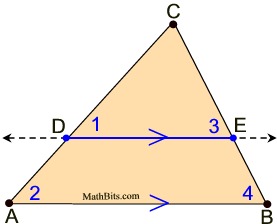
Proof of Side Splitter Theorem and its Converse
|
(Side Splitter Theorem): If a line is parallel to a side of a triangle and intersects the other two sides, then this line divides those two sides proportionally. (proof below) |
|
While this theorem may look somewhat like the "mid-segment" theorem, the segment  in this theorem does not necessarily connect the "midpoints" of the sides. in this theorem does not necessarily connect the "midpoints" of the sides.
Proof:
Statements |
Reasons |
|
1. Given |
|
2. If 2 || lines are cut by a transversal, the corresponding angles are congruent. |
|
3. (AA) If two ∠s of one Δ are congruent to the corresponding ∠s of another Δ, the Δs are similar. |
|
4. Corresponding sides of similar triangles are in proportion. |
|
5. Segment Addition Postulate (or whole quantity equals the sum of its parts) |
|
6. Substitution |
|
7. In a proportion, the product of the means = the product of the extremes. |
|
8. Distributive property |
|
9. Subtraction |
|
10. In a proportion, the product of the means = the product of the extremes. |

 Converse
Converse |
(Side Splitter Theorem): If a line intersects two sides of a triangle and divides the sides proportionally, the line is parallel to the third side of the triangle. |
|
Proof:
Statements |
Reasons |
|
1. Given |
|
2. In a proportion, the product of the means = the product of the extremes. |
|
3. Reflexive (Identity) |
|
4. Addition |
|
5. Distributive property |
|
6. In a proportion, the product of the means = the product of the extremes. |
|
7. Segment Addition Postulate (or whole quantity equals the sum of its parts) |
|
8. Substitution |
|
9. Reflexive (Identity)
|
|
10. (SAS for Similarity). In two triangles, if two sets of corresponding sides are proportional and the included angle is congruent, the triangles are similar. |
|
11. Corresponding angles of similar triangles are congruent. |
|
12. If 2 lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


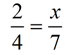 (form a proportion using the segment lengths)
(form a proportion using the segment lengths)