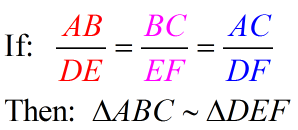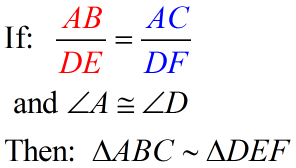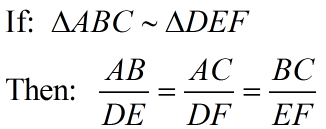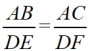|
We saw a series of shortcut methods for establishing that two triangle are congruent, without having to prove all 3 corresponding angles are congruent and all 3 corresponding sides are congruent. These shortcut methods included SSS, ASA, SAS, AAS and HL
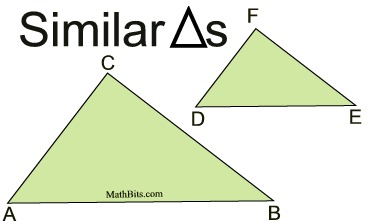
So, how do we prove triangles similar?
|
Two triangles are similar if and only if the corresponding sides are in proportion and the corresponding angles are congruent. |
|
Fortunately, we also have shortcut methods for establishing that two triangles are similar, without having to prove all 3 corresponding angles are congruent and all 3 sets of corresponding sides are in proportion. These shortcut methods include AA, SSS, and SAS.
Wow! Some of the same "letterings", but not the same "theorems".
Let's take a look!

| There are three accepted methods for proving triangles similar: |
While three methods exist, the AA Similarity Theorem is by far the most popular method.
Always look for the AA method first.
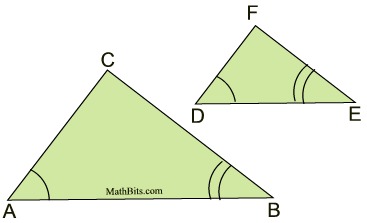
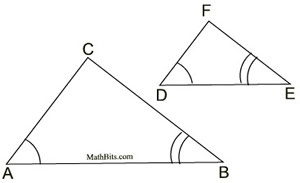
AA Similarity Theorem:
AA for
similar triangles |
To prove two triangles are similar, it is sufficient to show that two angles of one triangle are congruent to the two corresponding angles of the other triangle. |
|
If two angles of one triangle are congruent to the corresponding angles of another triangle, the triangles are similar. (proof of this theorem is shown below) |
|
|
Yes, this could also be AAA. But if you have 2 sets of angles, you automatically have the 3rd set.
So, proving 2 sets congruent is sufficient to prove similar triangles.

  
The next two methods for proving similar triangles are
NOT the same theorems used to prove congruent triangles. |
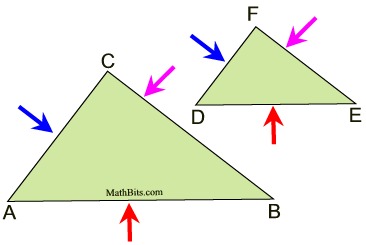
SSS Similarity Theorem:
SSS
for similar triangles |
To prove two triangles are similar, it is sufficient to show that the three sets of corresponding sides are in proportion. |
|
If the three sets of corresponding sides of two triangles are in proportion, the triangles are similar. (proof of this theorem is shown below) |
|
|

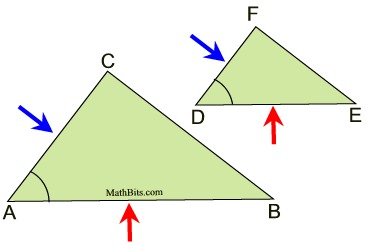
SAS Similarity Theorem:
SAS for similar triangles |
To prove two triangles are similar, it is sufficient to show that two sets of corresponding sides are in proportion and the angles they include are congruent. |
|
If an angle of one triangle is congruent to the corresponding angle of another triangle and the lengths of the sides including these angles are in proportion, the triangles are similar. (proof of this theorem is shown below) |
|
|

Remember, how, after proving triangles congruent, we could state that the "left-over parts"
that were not directly used would also be congruent?
CPCTC - Corresponding parts of congruent triangles are congruent.
We can also use this idea of "left-over parts" when working with similar triangles.
After proving the triangles similar by AA, we can state:
Corresponding sides of similar triangles are in proportion.
The "angles" have already been addressed in AA, so they are not mentioned.
This statement is just a reiteration of part of the definition of similar triangles.
You might think the letters CSSTP may be used, but letters are not traditionally assigned to this statement.
Once the triangles are similar by AA ...
the remaining set of angles will be congruent and the remaining corresponding sides will be in proportion. Just be sure the triangles are similar before using the following statement. |
| Corresponding sides of similar triangles are in proportion. |
|
|
When working with similar triangle proofs, we will even be going one step further and
"cross-multiplying" the proportions to form products.
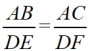 |
• Corresponding sides of similar triangles are in proportion. |
| DE • AC = AB • DF |
• In a proportion, the product of the means equals the product of the extremes. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

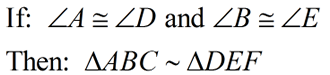
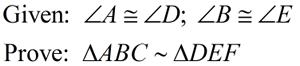
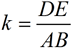 . The new dilated triangle will be ΔA'B'C'.
. The new dilated triangle will be ΔA'B'C'.