|
The use of similar triangles appears in the solutions to many different types of mathematical problems. The good news is that there are often several different ways to arrive at answers to these problems. Keep an open mind, and be on the look out for the possibility of several different solution methods. |
|
|
When working with numerical (or algebraic) problems and similar triangles,
you are most likely working with proportions.
If you need a quick review of "ratios and proportions", see "Refresher: Ratios and Proportions".
Consider the following strategies using similar triangles:
All of the triangles used in these examples can be shown to be similar by AA.
Situation 1: Two separate, marked triangles
|
 The triangles seen in this problem are positioned such that their corresponding parts are in the same positions in each triangle. If the triangles are not positioned in this manner, you can match the corresponding sides by looking across from the angles which are marked to be congruent (or known to be congruent) in each triangle. The triangles seen in this problem are positioned such that their corresponding parts are in the same positions in each triangle. If the triangles are not positioned in this manner, you can match the corresponding sides by looking across from the angles which are marked to be congruent (or known to be congruent) in each triangle. |
|
Situation 2: Overlapping triangles (a popular diagram for similar triangles)
|
Is ΔABC similar to ΔDBE?
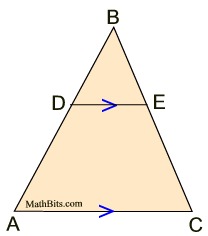 |
Many problems involving similar triangle have one triangle on top of (overlapping) the other.
In this diagram, it is indicated that
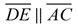 . .
Since ∠A is congruent to ∠BDE (corresponding ∠s from the || lines), and ∠B is shared by both triangles, we have similarity of the triangles by AA.
So, YES, the triangles are similar.
|
Now, if you are asked to find a missing side (or segment) in this overlapping situation,
you have two solution methods to consider:
Use FULL sides from the two triangles.
Do not use DA or EC in your proportion since they are not the lengths of SIDES of the triangles.
When in doubt, use this method!
|
Use Side Splitter Theorem:
"If a line is parallel to one side of a triangle, and intersects the other two sides, the line divides these two sides proportionally."
This method may not apply in all situations. |
The choice of which method to use will depend upon the given information regarding the sides, what you are asked to find, and which method you feel most secure in using. |
|
|
Situation 3: Find side of triangle given lengths that are not sides of triangles
|
Find BE.
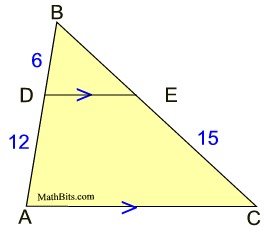 |
Always read carefully to see WHAT you are supposed to find. This question asks you to find BE, which is a length of a side of a triangle.
From Situation 2, we know these triangles are similar.
Consider these two possible solution methods,
letting BE = x:
Use FULL sides
of the triangles:
(do not use 12 or 15
as they are not sides of a triangle)
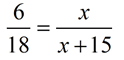 6x + 90 = 18x
6x + 90 = 18x
90 = 12x
7.5 = x
|
Use Side Splitter Theorem:
(since we have "non-triangle sides" segments)
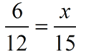
90 = 12x
7.5 = x
|
|
|
|
Situation 4: Find segment that is not the side of a triangle
|
Find EC.
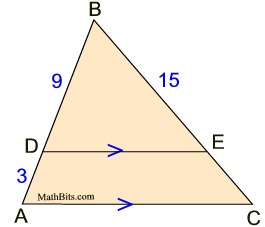 |
This question asks you to find EC, which is not a length of a side of a triangle.
From Situation 2, we know these triangles are similar.
Consider these two possible solution methods,
letting EC = x:
Use FULL sides
of the triangles:
(do not use 3 or x by itself
as they are not sides of a triangle)
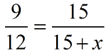 135 + 9x = 180
135 + 9x = 180
9x = 45
x = 5
|
Use Side Splitter Theorem:
(since we have "non-triangle sides" segments)
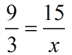
9x = 45
x = 5
|
|
|
|

Just when the "Side Splitter Theorem" method was looking like the easier method ...
Situation 5: BE CAREFUL here!!
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|