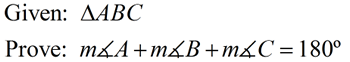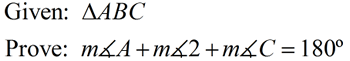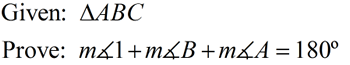|
 |
The sum of the measures of the interior angles of a triangle equals 180º. |
|
1.  |
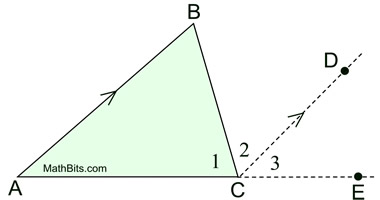
Find m∠B
and m∠C. |
Solution:
m∠A + m∠B + m∠C = 180
38 + x + (x + 2) = 180
40 + 2x = 180
2x = 140
x = 70 = m∠B
x + 2 = 72 = m∠C |
2. The angles in a triangle are represented by (4x - 6)º, (2x + 1)º and (x + 3)º. Is this a right triangle? |
Solution:
(4x - 6) + (2x + 1) + (x + 3) = 180
7x - 2 = 180
7x = 182
x = 26
(4x - 6)º = 98º
(2x + 1)º = 53º
(x + 3)º = 29º
No. The triangle is obtuse. |
3. |
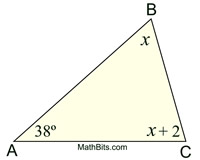
m∠ABC=m∠BCD
Find m∠ACD. |
Solution: m∠BCD = 56º.
In ΔABC, 85º + 56º + m∠BCA = 180
m∠BCA = 39º
m∠ACD = 56º - 39º = 17º
|
4. The angles in a triangle are in the ratio of 1 : 2 : 3. Find the measure of the angles in the triangle.
Solution:
x + 2x + 3x = 180
6x = 180
x = 30
The angles are 30º, 60º, and 90º.
|

In your previous studies of this theorem, you most likely saw how a triangle's angles can be cut off and rearranged to form a straight angle of 180º (as shown below).

We now need to use more sophisticated ideas to establish that this theorem is actually true. Throughout history, several different methods of proof of this theorem have appeared.
Let's take a look at a few of these methods of proof.
Transformational Proof Using Translation |
 [Also written as m∠A + m∠ABC + m∠C = 180.]
[Also written as m∠A + m∠ABC + m∠C = 180.] |
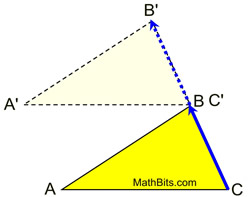 |
Proof:
• Translate ΔABC so C' coincides with B forming a straight line from point C, through point B, to point B' (along vector 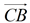 ). ).
•
Since translations are rigid transformations, we know that angle measure is preserved making m∠C = m∠A'BB'.
•
A straight angle, ∠B'BC, whose measure by definition is 180º, exists giving
m∠A'BB' + m∠A'BA + m∠ABC = 180.
•
Angles ∠C and ∠A'BB' are congruent corresponding angles making 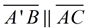 . It can also be said that these sides are parallel because in a translation the corresponding segment sides of the pre-image and image are parallel. . It can also be said that these sides are parallel because in a translation the corresponding segment sides of the pre-image and image are parallel.
•
As a result, ∠A and ∠A'BA are congruent alternate interior angles. If 2 parallel lines are cut by a transversal, the alternate interior angles are congruent.
•
By substitutions, m∠C + m∠A + m∠ABC = 180.
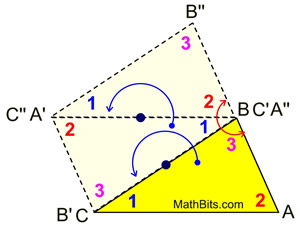
Transformational Proof Using Rotation |
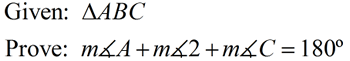
[Or m∠ABC + m∠ACB + m∠BAC = 180.]
|
|
Proof:
• Rotate ΔABC about the midpoint of 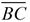 . .
•
Then rotate ΔA'B'C' about the midpoint of 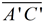 . .
•
Since rotations are rigid transformations, angle measure is preserved and m∠ABC = m∠A'B'C' and m∠B'A'C' = m∠B''A''C''.
•
These alternate interior angles will be congruent, making 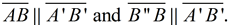 If 2 lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel.
• Since both 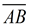 and and 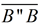 pass through point B and are parallel to pass through point B and are parallel to 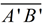 , we know the segment from A to B'' is straight (there is only one line through B parallel to , we know the segment from A to B'' is straight (there is only one line through B parallel to 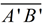 - Parallel Postulate). - Parallel Postulate).
•
A straight angle is an angle whose rays form a straight line, making ∠ABB'' a straight angle with a measure of 180º.
Now, m∠ABC + m∠A'BB' + m∠B''BA' = 180.
•
Rotations preserve angle measure, making m∠A'BB' = m∠ACB and m∠BAC = m∠BA'C = m∠A'BB''.
•
By substitution, m∠ABC + m∠ACB + m∠BAC = 180.
Traditional (Classical) Proofs: |
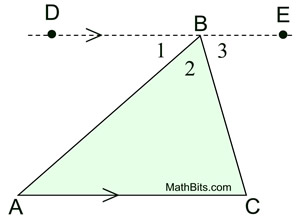
Proof Using An Auxiliary Parallel Line |
Statements |
Reasons |
1. ΔABC |
1. Given |
2. Draw auxiliary line through B parallel to 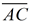 . |
2. Through a point not on a line, only one line may be drawn parallel to a given line. |
3. ∠DBE is a straight angle. |
3. A straight line forms a straight angle. |
4. m∠DBE = 180º |
4. A straight angle has a measure of 180º. |
5. m∠1 + m∠2 + m∠3 = m∠DBE |
5. Angle Addition Postulate (whole quantity) |
6. 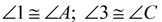 |
6. If 2 parallel lines are cut by a transversal, the alternate interior angles are congruent. |
7. m∠1 = m∠A; m∠3 = m∠C |
7. Congruent angles are angles of equal measure. |
8. m∠A + m∠2 + m∠C = 180º |
8. Substitution |
Slightly different version:
Proof Using An Auxiliary Parallel Line with an Extension |
Statements |
Reasons |
1. ΔABC |
1. Given |
2. Extend 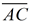 through C to E, and draw an auxiliary line through C parallel to 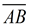 . |
2. Through a point not on a line, only one line may be drawn parallel to a given line. |
3. ∠ACE is a straight angle. |
3. A straight line forms a straight angle. |
4. m∠ACE = 180º |
4. A straight angle has a measure of 180º. |
5. m∠1 + m∠2 + m∠3 = m∠ACE |
5. Angle Addition Postulate (whole quantity) |
6. 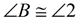 |
6. If 2 parallel lines are cut by a transversal, the alternate interior angles are congruent. |
7. 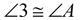 |
7. If 2 parallel lines are cut by a transversal, the corresponding angles are congruent. |
7. m∠B = m∠2; m∠3 = m∠A |
7. Congruent angles are angles of equal measure. |
8. m∠1 + m∠B + m∠A = 180º |
8. Substitution |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|