|
There are some special relationships between "pairs" of angles.
 Adjacent Angles are two angles that share a common vertex, a common side, and no common interior points. (They share a vertex and side, but do not overlap.)
|
|
∠1 and ∠2 are adjacent angles.
∠ABC and ∠1 are NOT adjacent angles.
(∠ABC overlaps ∠1.) |
A Linear Pair is two adjacent angles whose non-common sides form opposite rays. |
|
∠1 and ∠2 form a linear pair.
The line through points A, B and C is a straight line.
∠1 and ∠2 are supplementary.
|
|
If two angles form a linear pair, the angles are supplementary.
A linear pair forms a straight angle which contains 180º, so you have 2 angles whose measures add to 180, which means they are supplementary. |
|
|
If two congruent angles form a linear pair, the angles are right angles.
If two congruent angles add to 180º, each angle contains 90º, forming right angles. |
|
|
Vertical Angles are two angles whose sides form two pairs of opposite rays (straight lines). |
|
Vertical angles are located across from one another in the corners of the "X" formed by the two straight lines.
∠1 and ∠2 are vertical angles.
∠3 and ∠4 are vertical angles.
Vertical angles are not adjacent.
∠1 and ∠3 are not vertical angles (they are a linear pair).
Vertical angles are always equal in measure. |
|
Vertical angles are congruent.
Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m∠1 + m∠4 = 180 and m∠2 + m∠4 = 180. With substitution, m∠1 = m∠2 and they are congruent. |
|
|
Complementary Angles are two angles the sum of whose measures is 90º. |
|
Complementary angles can be placed so they form perpendicular lines, or they may be two separate angles.
∠1 and ∠2 are complementary.
∠P and ∠Q are complementary.
|
|
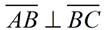
Complements of the same angle, or congruent angles, are congruent.
If m∠a is complementary to the m∠b, and m∠c is complementary to m∠b, then
m∠a = m∠c. Consider m∠a = 60º, m∠b = 30º and m∠c = 60º. |
|
|
The acute angles of a right triangle are complementary.
The sum of the angles in a triangle add to 180º. After subtracting 90º for the right angle, there are 90º left for the two acute angles, making them complementary. |
|
|
Supplementary Angles are two angles the sum of whose measures is 180º. |
|
Supplementary angles can be placed so they form a linear pair (straight line), or they may be two separate angles.
∠1 and ∠2 are supplementary.
∠P and ∠Q are supplementary.
The line through points A, B and C is a straight line. |
|
Supplements of the same angle, or congruent angles, are congruent.
If m∠a is supplementary to the m∠b, and m∠c is supplementary to m∠b, then
m∠a = m∠c. Consider m∠a = 60º, m∠b = 120º and m∠c = 60º. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
