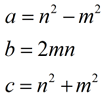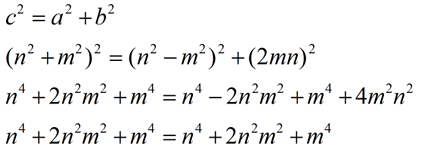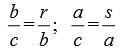|
While the Babylonians understood the relationship regarding the sides of a right triangle nearly 1,000 years before Pythagoras, it was Pythagoras that first "proved" the concept.
Pythagoras popularized the relationship between the hypotenuse and the legs of a right triangle, and discovered that this relationship is true for ALL right triangles.
As the first mathematician to geometrically prove this theorem, the theorem bears his name.
|
 Pythagoras
Pythagoras 500 BC
Greek Mathematician |
 |
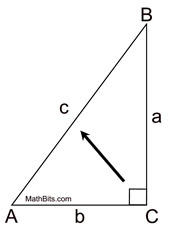
Pythagorean Theorem: In any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. |
|
Pythagorean Theorem
c2 = a2 + b2
for any right triangle
a and b are "legs"
c is the "hypotenuse"
(c is across from the right angle)
|
|

|
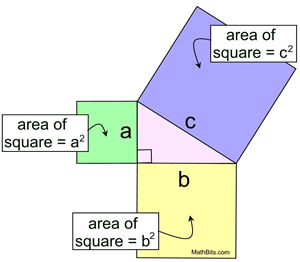
The Pythagorean Theorem can be interpreted in relation to squares drawn to coincide with each of the sides of a right triangle, as shown at the right.
The theorem can be rephrased as, "The (area of the) square described upon the hypotenuse of a right triangle is equal to the sum of the (areas of the) squares described upon the other two sides."
|
 |

There are specific sets of positive integer values that have a special connection to the Pythagorean Theorem. These sets not only satisfy the Pythagorean Theorem, but multiples of these integers also satisfy the Pythagorean Theorem.
For example, the numbers 3, 4, 5 satisfy the Pythagorean Theorem: 32 + 42 = 52.
If you multiply all of these numbers by 2, you get 6, 8, 10 which also satisfy the Pythagorean Theorem:
62 + 82 = 102. Multiplying 3, 4, 5 by the same positive integer value will create a new set of integers that will also satisfy the Pythagorean Theorem.
If a, b and c are positive integers that satisfy the Pythagorean Theorem, then ka, kb and kc, where k is a positive integer, will also satisfy the Pythagorean Theorem.
The special sets of integers that possess this property are called "Pythagorean Triples".
Three of the most common Pythagorean Triples are
3, 4, 5 |
5, 12, 13 |
8, 15,17 |
Computer programmers use equations to generate lists of Pythagorean Triples:
When m and n are both positive integers and m < n, Pythagorean Triples can be generated using the following equations where a and b will be the legs of the right triangle and c will be the hypotenuse.
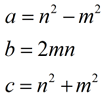
It can be shown that the results from these equations do, in fact, satisfy the Pythagorean Theorem:
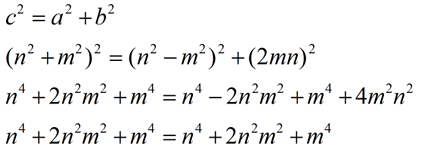

If we reverse the "if" and "then" concepts of the Pythagorean Theorem, we will get the "converse" of the Pythagorean Theorem which is also a theorem used to prove a triangle is a right triangle.
 |
(Converse): If the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, the triangle is a right triangle. |
|

| PROOF of Pythagorean Theorem: |
There are literally hundreds of geometrical and algebraic proofs of the Pythagorean Theorem.
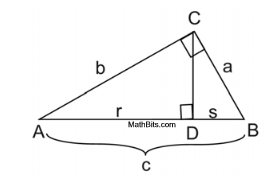
Let's take a look at a proof using similar triangles.
Statements |
Reasons |
1. |
|
1. |
Given |
2. |
|
2. |
The altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side. |
3. |
|
3. |
Perpendicular lines form right angles. |
4. |
|
4. |
A right triangle contains one right angle. |
5. |
|
5. |
All right angles are congruent. |
6. |
|
6. |
Reflexive (Identity) |
7. |
|
7. |
AA Theorem for Similarity |
8. |
|
8. |
Corresponding sides of similar triangles are in proportion. |
9. |
|
9. |
In a proportion, the product of the means = the product of the extremes. |
10. |
|
10. |
Addition |
11. |
|
11. |
Distributive property in reverse |
12. |
|
12. |
Whole quantity = sum of parts. |
13. |
|
13. |
Substitution |
14. |
|
14. |
Multiplication |

The Pythagorean Spiral (also called the Square Root Spiral or the Spiral of Theodorus) is shown at the right.
The spiral is a series of right triangles, starting with an isosceles right triangle with legs of length one unit. Another right triangle is built upon the first triangle with one leg being the hypotenuse from the previous triangle and the other leg having a length of one unit. This process is then repeated.
Most diagrams of the spiral stop with the hypotenuse being 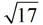 , as the next right triangle will overlap the starting triangle. , as the next right triangle will overlap the starting triangle. |
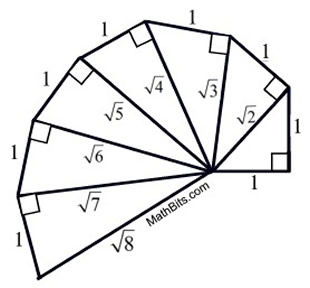 |
The spiral can be extended beyond the hypotenuse of 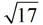 and the triangles will begin to overlap previous triangles. In 1958, Erich Teuffel proved that while the triangles may overlap, no two hypotenuses will ever coincide, no matter how far the spiral is continued. and the triangles will begin to overlap previous triangles. In 1958, Erich Teuffel proved that while the triangles may overlap, no two hypotenuses will ever coincide, no matter how far the spiral is continued. |

| Mathematical Connections: |
• Connection to the Distance Formula: The Pythagorean Theorem serves as the basis for determining the distance between two points in the Cartesian plane (coordinate axis), called the Distance Formula.
 |
If (x1, y1) and (x2, y2) are points in the plane, then the distance between them can be determined using the Pythagorean Theorem.

|
• Generalization of the Law of Cosines: The Pythagorean Theorem is a specific case of the more general theorem relating the lengths of sides in any triangle, called the Law of Cosines.
Law of Cosines: 
When angle C is 90º, cosC equals 0 and the formula becomes the Pythagorean Theorem.
• In non-Euclidean Geometry: While the Pythagorean Theorem is of prime importance in Euclidean Geometry (and is derived from its axioms), it does not hold in non-Euclidean Geometries.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|