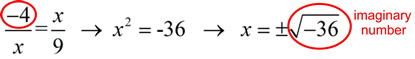|
The term "mean proportional" may also be referred to as "geometric mean".
The term "mean", when used alone, or in a context such as "mean, median, and mode",
refers to finding the "average" and is known as the Arithmetic Mean.
Mean proportional, or geometric mean, is not the same as the Arithmetic Mean. While an arithmetic mean deals with addition, a geometric mean deals with multiplication.
|
The mean proportional, or geometric mean, of two positive
|
numbers a and b is the positive number x such that 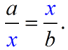 When solving, 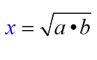 . |
Notice that the x value appears TWICE in the "means" positions of the proportion. |
|
Note*: The mean proportional (geometric mean), along with the values of a and b, are positive.
Mean
Proportional
or
Geometric Mean

|
|
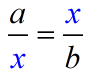
In a "mean proportional", or "geometric mean", both " means" ( x) are the exact same value. |
|
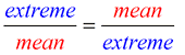 Remember the rule:
In a proportion, the product of the means equals the product of the extremes ("cross multiply").
Remember the rule:
In a proportion, the product of the means equals the product of the extremes ("cross multiply"). |
|
Examples:
1. |
Find the mean proportional between 2 and 18? |
| |
|
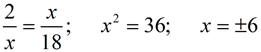 While algebraically there are two solutions for x,
While algebraically there are two solutions for x,
the mean proportional, by definition, is positive.
Answer: x = 6 |
Check answer:
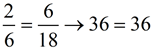
|
2. |
What is the geometric mean of 6 and 12? |
| |
|
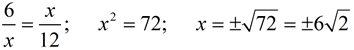 Remember, the geometric mean of two positive numbers is positive.
Remember, the geometric mean of two positive numbers is positive.
 |
Check answer: 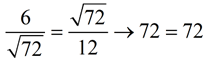 |
You can see from Example 2 that it will be necessary to remember your skills for
working with radicals. If you need a refresher, go to the "Radicals" section under Algebra 1.

3. |
The mean proportional between two values is 8. If one of the values is 16, find the other value. |
| |
|
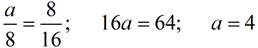 Answer: a = 4
Answer: a = 4 |
Check the answer:
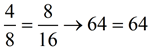 |

* FYI: (More information about the DEFINITON of geometric mean or mean proportional)
 |
In the most general sense, a geometric mean is a type of mean which indicates the central tendency, or "typical value", of a set of numbers by using the "product" of the values in the set. If all of the numbers in the set are replaced by the same value, what would that value have to be to produce the same product as the product of the numbers in the original set? This "replacement value" is the geometric mean. |
There are a variety of definitions of "geometric mean" which fall into 3 basic categories:
(These definitions are quoted from various mathematics textbooks.)
| Category 2 (variety of definitions relating to n numbers): |
 (Definition 1) The geometric mean is the nth root of the product of n numbers. (Definition 1) The geometric mean is the nth root of the product of n numbers.
 (Definition 2) The geometric mean is the nth positive root of the product of n positive given values. (Definition 2) The geometric mean is the nth positive root of the product of n positive given values.
| Category 3 (variety of definitions relating to geometric sequences): |
 (Definition 1) The geometric mean is the term between any two nonconsecutive terms of a geometric sequence. (Definition 1) The geometric mean is the term between any two nonconsecutive terms of a geometric sequence.
 (Definition 2) The geometric mean is the central number in a geometric sequence. (Definition 2) The geometric mean is the central number in a geometric sequence.
 (Definition 3) The geometric mean of a and b is a number x such that a, x, and b form a geometric sequence. Then (Definition 3) The geometric mean of a and b is a number x such that a, x, and b form a geometric sequence. Then 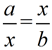 so x2 = ab and the geometric mean = so x2 = ab and the geometric mean =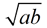 or or 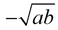 . .
Notice the discrepancies between the definitions regarding the positive nature of the terms involved. Some definitions identify the need for "positive" values, while other definitions do not. |
 |
A general consensus seems to be that the geometric mean is only "well defined" for sets of positive real numbers, with the geometric mean also being positive. Should either a or b in 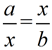 be negative, their product, ab, will be negative, and the geometric mean will be the square root of a negative value, which is an imaginary number. be negative, their product, ab, will be negative, and the geometric mean will be the square root of a negative value, which is an imaginary number.
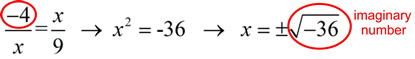
Most uses of the geometric mean involve positive real data, such as the length of the sides of a geometric figure, the number of students responding to a survey, a rate of interest, or population growth. Thus, a representative geometric mean in these situations will be positive.
So, what does all of this mean?
It means that since we will be working with geometric figures and primarily the lengths of the sides of these figures, this web site will be using a definition that refers to the geometric mean (or mean proportional), as a positive quantity, dealing with positive values.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

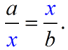 When solving,
When solving, 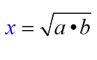 .
. 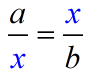
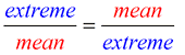
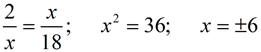
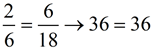
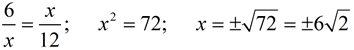
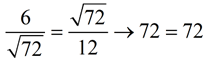
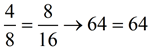

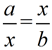 so x2 = ab and the geometric mean =
so x2 = ab and the geometric mean =