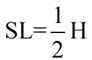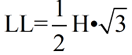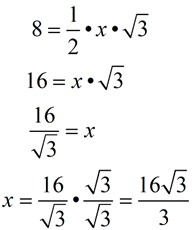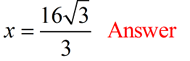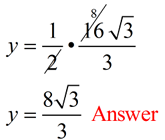|
There are two "special" right triangles that will continually appear throughout your study of mathematics: the 30º-60º-90º triangle and the 45º-45º-90º triangle. The special nature of these triangles is their ability to yield exact answers instead of decimal approximations when dealing with trigonometric functions. This page will deal with the 30º-60º-90º triangle.
All 30º-60º-90º triangles are similar!
They satisfy Angle -Angle (AA) for proving triangles similar. |
Create a 30º-60º-90º triangle for investigation: |
Congruent 30º-60º-90º triangles are formed when an altitude is drawn in an equilateral triangle. Remember that the altitude in an equilateral triangle will bisect the angle and is the perpendicular bisector of the side. If the side of the equilateral triangle is set to a length of 2 units, the Pythagorean Theorem will find the length of the altitude to be 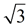 units. units. |
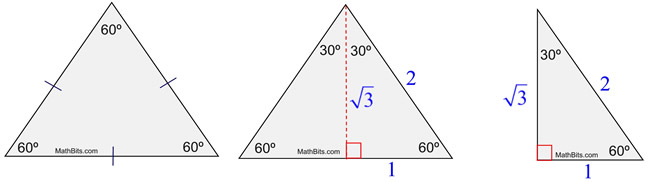 Note: the side of the equilateral triangle need not be a length of 2 for the patterns to emerge.
Note: the side of the equilateral triangle need not be a length of 2 for the patterns to emerge.
The choice of a side length of 2 simply makes the calculations easier.
Yes, 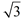 is smaller than 2, making the hypotenuse of 2 the longest side. Remember 2 can be written as 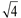 .
 |
You have now seen "how" to generate the side lengths of a
30º-60º-90º triangle from an equilateral triangle. If you can remember this relationship, you will be able to tackle any question pertaining to 30º-60º-90º triangles.
|
|
Once the sides of the 30º-60º-90º triangle are established, a series of relationships (patterns) can be identified between the sides of the triangle. ALL 30º-60º-90º triangles will possess these same patterns. These relationships will be referred to as "short cut formulas" that can quickly answer questions regarding side lengths of 30º-60º-90º triangles, without having to apply any other strategies such as the Pythagorean Theorem or trigonometric functions.
|
Short Cut Pattern Formulas: |
Since 30º-60º-90º triangles are similar, their corresponding sides are proportional. As such, we can establish a pattern as to how their sides are related. The following pattern formulas will let you quickly find the sides of a 30º-60º-90º triangle even when you are given only ONE side of the triangle. Remember, these formulas work ONLY in a 30º-60º-90º triangle!
Labeling: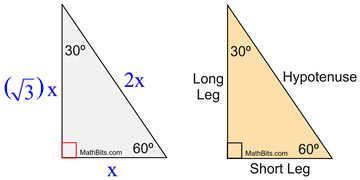
H = Hypotenuse
LL = Long Leg (across from 60º)
SL= Short Leg (across from 30º)
|
|
|
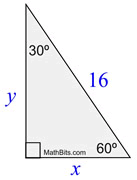
This example shows the easiest application of the patterns (where the hypotenuse is given).
Always look at what is "given" and what you need to find.
1. |
Find x and y.
|
x is the short leg
(across from the 30º angle)
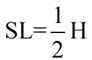
x = ½ • 16
x = 8Answer
|
|
This example requires more thinking and more algebraic work (where the short leg is given).
Always start with what is "given" and work from that point.
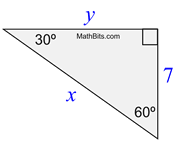
2. |
Find x and y.
|
7 is the short leg
(x is the hypotenuse)
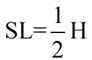
7 = ½ • x
x = 14 Answer
|
|
This example requires the most algebraic and radical work (where long leg is a given integer).
Since the "given" is the long leg, start with the long leg.
3. |
Find x and y.
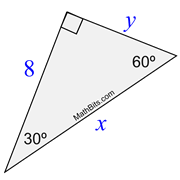
This example shows that working with radicals is a needed skill.
To remove a radical value from a denominator, multiply (top and bottom) by that radical value.
Radical Review
|
8 is the long leg
(x is the hypotenuse)
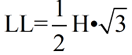
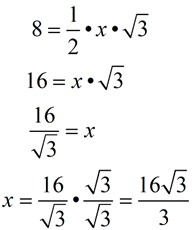
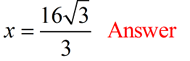
|
y is the short leg
(use hypotenuse you found)
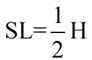
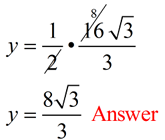
These answers are "exact" answers. "Approximate" answer using your calculator will be
x = 9.24 and y = 4.62 to nearest hundredth. |
|
 |
Notice that when you are working with a 30º-60º-90º triangle
you are working with 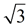 .
Look at all of the THREEs at work! 30, 60, 90, 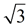 When you work with
30º-60º-90º and 45º-45º-90º triangles,
When you work with
30º-60º-90º and 45º-45º-90º triangles,
you will need to keep straight which radical goes with which triangle.
|
I forgot the formula patterns! Now what?
Remember that there is always more than one way to attack a problem!
If you forget these formula patterns, you can use trigonometry functions and/or the Pythagorean Theorem to find the missing sides. Be warned, however, that the Pythagorean Theorem by itself, will not help you find both missing sides, since the Pythagorean Theorem needs two sides to work. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|