|
A quadrilateral is a four-sided polygon. |
|
All quadrilaterals are coplanar and have two diagonals.
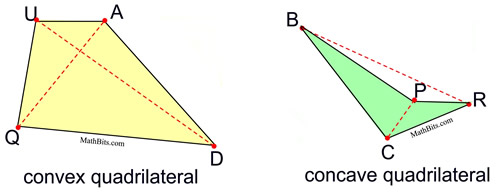
Quadrilaterals may be drawn in a "convex" form or a "concave" form. The quadrilaterals we will be using will be convex, where the diagonals lie within the figure. A concave quadrilateral contains an angle greater than 180º, and at least one of the diagonals lies partially, or entirely, outside of the figure (as shown below). The concave figure "caves in" upon itself.
|
The sum of the measures of the four angles of any quadrilateral equals 360º. |
|
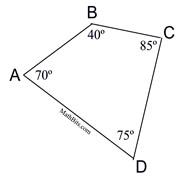
In the diagram at the right,
m∠A + m∠B + m∠C + m∠D = 360º.
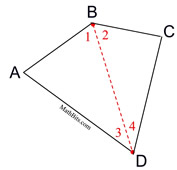
Every quadrilateral can be decomposed into two triangles, each of whose angles' measures sum to 180º.
m∠A + m∠1 + m∠ 3 = 180º
m∠C + m∠2 + m∠4 = 180º
m∠A+m∠1+m∠3+m∠C+m∠2+m∠4 = 360º |
  |

There are several "types" of quadrilaterals determined by their characteristics, or properties.
We will be examining three types of quadrilaterals: parallelograms, trapezoids and kites.
|
A parallelogram is a quadrilateral with both pairs of opposite sides parallel. |
|
There are three additional quadrilaterals that possess the properties of a parallelogram.
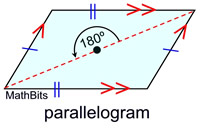 There are 6 properties you need to remember about parallelograms.
There are 6 properties you need to remember about parallelograms.
|
Properties:
Definition: A parallelogram has two pairs of parallel sides.
• A parallelogram has opposite sides parallel.
• A parallelogram has opposite sides congruent.
• A parallelogram has opposite angles congruent.
• A parallelogram has consecutive angles supplementary.
• A parallelogram has diagonals bisecting each other.
• A parallelogram has diaagonals forming 2
 triangles.
---------------------------------------------------------------------
Symmetry:
• A parallelogram has no reflectional symmetry.
• A parallelogram has rotational symmetry of 180º (Order 2).
|
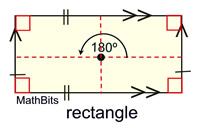 A rectangle has the 6 properties of a parallelogram PLUS 2 more.
A rectangle has the 6 properties of a parallelogram PLUS 2 more. |
Properties:
Definition: A rectangle is a parallelogram with 4 right angles.
A rectangle has the 6 properties of a parallelogram, plus:
•
A rectangle also has four right angles.
• A rectangle has congruent diagonals.
---------------------------------------------------------------------
Symmetry:
• A rectangle has two axes of reflectional symmetry.
• A rectangle has rotational symmetry of 180º (Order 2).
|
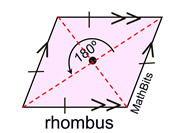
A rhombus has the 6 properties of a parallelogram PLUS 3 more.
|
Properties:
Definition: A rhombus is a parallelogram with 4 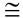 sides.
A rhombus has the 6 properties of a parallelogram, plus:
• A rhombus has all four sides congruent.
• A rhombus has diagonals that bisect the angles.
• A rhombus has diagonals that are perpendicular.
---------------------------------------------------------------------
Symmetry:
• A rhombus has 2 (diagonals) axes of reflectional symmetry.
• A rhombus has rotational symmetry of 180º (Order 2). |
Properties:
6 from parallelogram
2 from rectangle
3 from rhombus.
|
Properties:
Definition: A square is a parallelogram with 4  sides and 4 right angles.
A square has the 6 properties of a parallelogram,
plus the 2 additional properties of a rectangle,
and the 3 additional properties of a rhombus.A
It has ALL of the properties.
---------------------------------------------------------------------
Symmetry:
• A square has four axes of reflectional symmetry.
• A square has rotational symmetry of 90º (Order 4). |
|
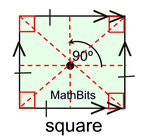
A trapezoid is a quadrilateral with at least one pair of parallel sides.
(meaning it could have "one pair" or "two pairs")
|
|
There are two basic types of trapezoids: regular trapezoids and isosceles trapezoids.
A trapezoid has 2 properties that you need to know. |
Properties:
Definition: A trapezoid has at least 1 pair of parallel sides.
• A trapezoid has at least 1 pair of parallel sides.
• The median of a trapezoid is parallel to the bases and half the sum of lengths of the bases.
--------------------------------------------------------------------
Symmetry:
• A trapezoid has no axes of reflectional symmetry.
• A trapezoid has no rotational symmetry (Order 1).
Note: Having no rotational symmetry means that the figure must be rotated a full 360º to again appear in it original position. This may be referred to as the identity symmetry.
|
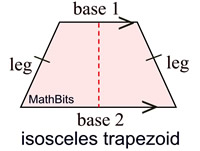
An isosceles trapezoid has the 2 properties of a trapezoid PLUS 4 more.
|
Properties:
Definition: An isosceles trapezoid is a trapezoid with congruent base angles.
• An isoscels trapezoid has at least one pair of parallel sides.
• The median of an isosceles trapezoid is parallel to the bases and half the sum of the lengths of the bases.
• An isosceles trapezoid has congruent legs.
• An isosceles trapezoid has congruent base angles.
• An isosceles trapezoid has congruent diagonals.
• An isosceles trapezoid has opposite angles supplementary.
--------------------------------------------------------------------
Symmetry:
• An isosceles trapezoid has at least 1 axis of reflectional symmetry. (If it has 2, it is a rectangle.)
• An isosceles trapezoid (with only 1 pair of parallel sides) has no rotational symmetry.
|
Note: The definition of an isosceles triangle states that the triangle has two congruent "sides".
But the definition of isosceles trapezoid stated above,
mentions congruent base "angles", not sides (or legs). Why?
If an isosceles trapezoid is defined to be "a trapezoid with congruent legs",
a parallelogram will be an isosceles trapezoid. If this occurs, the other properties that an isosceles trapezoid can possess can no longer hold,
since they will not be true for a parallelogram.
If we define an isosceles trapezoid to be a trapezoid with congruent base angles, we can easily prove the sides (legs) to also be congruent, a parallelogram will NOT be an isosceles trapezoid, and all of the commonly known properties of an isosceles trapezoid will still be true.

|
A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of adjacent, congruent sides. |
|
|
Properties:
• A quadrilateral kite resembles a flying kite.
• A kite has two pairs of adjacent sides of equal measure. Notice that these sides are not "opposite" sides.
---------------------------------------------------
Symmetry:
• The kite at the right has one vertical axis of reflectional symmetry,  . .
• The kite has no rotational symmetry. |
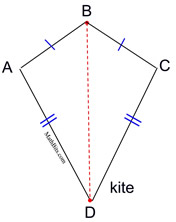 |
A kite also resembles a triangle reflected over one of its sides, forming a quadrilateral.
Notice ΔABD being reflected over its side from B to D, forming
ΔCBD.