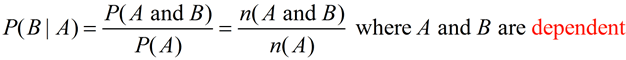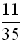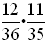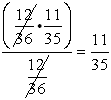|
The conditional probability of an event B, in relation to event A, is the probability that event B will occur given the knowledge that an event A has already occurred.
|
In plain English ...
you toss two pennies. The first penny shows HEADS and the other penny rolls under the table and you cannot see it. Now, what is the probability that they are both HEADS? Since you already know that one is HEADS, the probability of getting HEADS on the second penny is 1 out of 2.
The probability changes if you have partial information.
This "affected" probability is called conditional probability. |
Notation for conditional probability: P(B|A)
read ... the probability of B given A. |
To establish our formulas for conditional probability, we will need to revisit our previous discussion of independent and dependent events.
| • If events A and B are independent (where event A has no effect on the probability of event B), then the conditional probability of event B given event A is simply the probability of event B.
|
Example 1: Two colored dice (one white, one red) are rolled.
a. What is the probability of rolling "box cars" (two sixes)?
b. What is the probability of rolling "box cars" knowing the first toss is a six? |
 |
Answer:
a. The probability of getting "box cars" (two sixes) is  .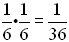
b. If, however, we roll the dice and see that the white die shows a six (and the red die is out of sight), the probability of the red die being six is  .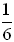
The probability of rolling "box cars", knowing that the first roll is a six, is .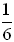
The probability changes when you have partial information about the situation.
|
| • If events A and B are dependent (where event A has effect on the probability of event B), then we saw that the probability that both events occur is defined by P(A and B) = P(A) • P(B | A).
Dividing both sides of this equation by P(A) gives us our formula for conditional probability of event B given event A, where event A affects the probability of event B:
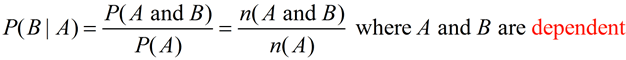Assuming P(A), n(A) are not zero.
|
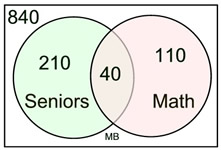
| Example 3: In a school of 1200 students, 250 are seniors, 150 students take math, and 40 students are seniors and are also taking math. What is the probability that a randomly chosen student who is a senior, is taking math? |
|
Answer: These questions can be confusing. It sounds, at first read, that they are asking for the probability of choosing a student who is a senior and who is taking math. Not quite right!
It helps to re-word the question into:
Find the probability that the student is taking math, given that the student is a senior.
B = the student is taking math
n(A) = the student is a senior = 250.
n(A and B) = the student is a senior and is taking math = 40.
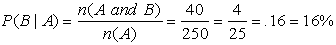
The answer is not 40/1200, because we already know the student is a senior.
|
 |
|
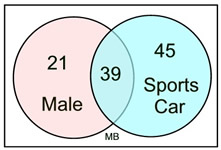
Example 4:
a) What is the probability of choosing a sports car given that the person is male?
|
Answer: We need to find P(Sports Car | male).
Now, the P(male) = 60/240 = 1/4 = 0.25
The P(Sports Car) = 84/240 = 0.35
But P(Sports Car | male) = 39/60 = 0.65
Remember that we KNOW the person is male, so the probability is the number of males choosing a Sports Care (39) divided by the number of males (60).
|
|
What happens if we reverse this order? Consider: |
|
| b) What is the probability of being a male given the chosen vehicle is a Sports Car? |
Answer: We need to find P(male | Sports Car).
Now, the P(male) = 60/240 = 1/4 = 0.25
The P(Sportscast) = 84/240 = 0.35
But P(male | Sports Car) = 39/84 ≈ 0.46
Remember that we KNOW the chosen vehicle is Sports Car, so the probability is the number of males choosing a Sports Care (39) divided by the number of Sports Cars (84). |
|
| The reversed order in a conditional probability does not yield the same result. It is not commutative. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
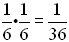
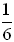