|
Permutation versus Combination |
Permutation: A set of objects in which position (order) is important.
To a permutation, the trio of Dottie, Alvin and Josie is DIFFERENT from Josie, Dottie, and Alvin.
Permutations are persnickety (picky)!
Combination: A set of objects in which position (or order) is NOT important.
To a combination, the trio of Dottie, Alvin and Josie is THE SAME AS Josie, Dottie, and Alvin. |
 |
Check out a few more comparisons of permutations and combinations:
Permutation |
Combination |
1. Pick a club President, Treasurer and Secretary from the members of the club. |
1. Pick three people from the members of the club. |
2. Pick your favorite flavor of ice cream and your least favorite flavor of ice cream, in this order, from a menu. |
2. Pick two flavors of ice cream from a menu. |
3. Pick first, second and third place winners. |
3. Pick three winners. |
Tidbit of Info:
|
|
The term "combination" lock is mathematically confusing. To open such a lock, the "order" of the digits entered IS very important, unlike a mathematical combination.
Perhaps, to be mathematically correct, it should be named a "permutation" lock! |

Formulas:
| A permutation is the choice of r things you want from a set of n things without replacement and where the order matters. |
|
|
| A combination is the choice of r things you want from a set of n things without replacement and where the order does not matters. (Notice the two forms of notations.) |
|
|

 Evaluate 7C2. Evaluate 7C2.
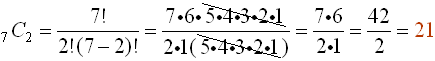
Notice how the cancellation occurs, leaving only 2 of the factorial terms in the numerator. A pattern is emerging ... when finding a combination such as the one seen in this problem, the second value (2) will tell you how many of the factorial terms to use in the numerator, and the denominator will simply be the factorial of the second value (2).
|

 There are 12 dogs and 14 cats at a shelter. Find the number of ways the shelter can select three of these animals to be in an advertising photo if they want two dogs and one cat. There are 12 dogs and 14 cats at a shelter. Find the number of ways the shelter can select three of these animals to be in an advertising photo if they want two dogs and one cat.
Order is not important in this problem.
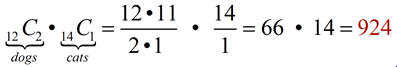
|

|
For working
with
combinations
on your
calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|