|
Directions: Read carefully. Choose the best answers.
1. |
All of the students in Mrs. Smith's classes belong to the Chorus, Band and/or Orchestra as shown in the Venn diagram at the right. If one student is chosen at random, what is the probability that the student belongs to the Chorus and the Band? |
|
|
|
2. |
All of the students in Mrs. Smith's classes belong to the Chorus, Band and/or Orchestra as shown in the Venn diagram at the right. If one student is chosen at random, what is the probability that the student belongs to the Chorus but not the Orchestra? |
|
|
|
3. |
What of the following choices can be illustrated by the Venn diagram at the right? |
|
|
|
4. |
An experiment is setup to first roll a die, followed by spinning a spinner. As shown, the die is a six-sided die and the spinner has four equal divisions labeled 1, 2, 3 and 4. Set A will contain all possibilities of the die rolling an even number and the spinner showing 4. Set B will contain all possibilities of the die and the spinner showing the same value. Find the probability of an outcome belonging to set A but not in set B.
|
|
|
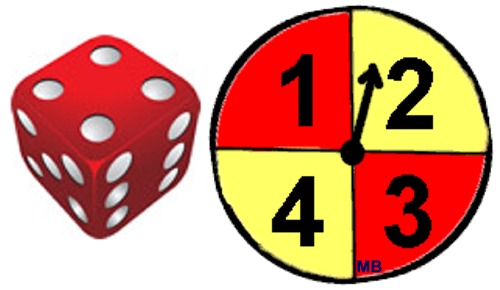 |
|
5. |
Given the Universal set to be integers 1 through 10.
Set A = integers that are multiples of 3.
Set B = even integers.
Use the Venn diagram to decide the value of the following probabilities: |
a) P(A)
b) P(A∩B)
c) P(B)C
d) P(A∪B)
e) P(A∩B)C
|
|
6. |
The freshman class has a population of 160 students. The number of freshman that play in the band is 54. The number of freshman that belong to a sports team is 90. If the probability that a student participates in the band or sports is 120/160, what is the probability that a student belongs to both the band and a sports team?
|
|
| |
|
7.
|
A veterinarian surveys 26 of his patrons. He discovers that 14 have dogs, 10 have cats, and 5 have fish. Four patrons have both dogs and cats. Three have dogs and fish. One has a cat and fish. If no one has all three kinds of pets, how many patrons have none of these pets?
|
 |
|
8. |
Two six-sided die are rolled. Considering all possible outcomes, what is the probability that the two rolled numbers have a product that is odd?
|
 |
|
|
9. |
In a class of 50 students, 18 take Chorus, 26 take Band, and 2 take both Chorus and Band. What is the probability that a student in the class is not enrolled in either Chorus or Band?
|
|
|
10. |
A guidance counselor is planning schedules for 30 students. Sixteen students say they want to take French, 16 want to take Spanish, and 11 want to take Latin. Five say they want to take both French and Latin, and of these, 3 wanted to take Spanish as well. Five wanted only Latin, and 8 wanted only Spanish. What is the probability that a student from this group of students wanted French only?
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|