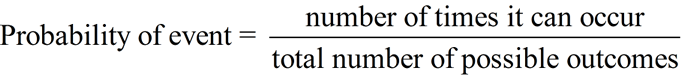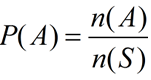Basic Concepts of Probability MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Probability is the chance that an event will occur. It is measured by the ratio of the favorable cases to the total number of cases possible.

A bit of history: It is said that the creation of the theory of probability occurred in 1654 over a dice game gambling dispute between two famous mathematicians, Blaise Pascal and Pierre de Fermat. A few years later, the first book on probability, as it related to gambling, was published.

The subject of probability developed rapidly during the 18th century with the contributions of other famous mathematicians. Over the following centuries, probability theory grew and expanded into a general discipline known as measure theory.

Outcomes are the possible results of an action.
Ratios are used to show how likely, or unlikely, an outcome might be.
Such a ratio is called the probability.

For example, the probability of getting heads on the toss of a penny is the ratio 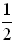. Heads is one of two possible outcomes when a penny is tossed.

The ratio for probability can be expressed as:

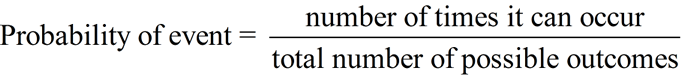
An event is a collection (subset) of outcomes of the sample space.
A simple event is an event with a single outcome.
A compound event is an event that is the joining together (union) of two or more simple events.

Ratios are most often expressed in the form of a fraction. Fractions, however, can also be expressed as decimals or percents. So probabilities may be expressed as fractions, decimals or percents.

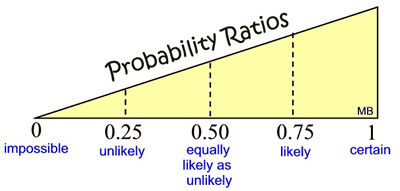	As the chart on the left shows, probabilities range from 0 to 1. If an event is impossible and will never occur, the probability is 0.  If an event is absolutely certain to occur, the probability is 1.  Otherwise, the value of a probability is between 0 and 1.
Events that are likely to occur have a probability greater than 0.50. Events that are not likely to occur have a probability less than 0.50.

While probability was originally developed to deal with gaming techniques, it is used today in a wide range of applications. Even common sayings reflect the concept of probability.

Someone says "Don't hold your breath" when you are waiting for something to happen.  What is the person implying about the probability that the event will occur in the near future?

Example: A fair die is rolled and the outcome noted. Determine whether each of the following outcomes is: certain to happen,   certain not to happen,   likely to happen,   likely not to happen.

Possible rolls: 1, 2, 3, 4, 5, 6	• rolling a 2	• probability = 1/6  likely not to happen
	• rolling a number less than 3	• probability = 1/6 + 1/6 = 2/6 likely not to happen
	• rolling a 7	• not possible - certain not to happen
	• rolling a number less than 10	• certain to happen
	• rolling a number greater than 1	• probability = 5/6   likely to happen
	• rolling a factor of 6 (1,2,3,6)	• probability = 4/6   likely to happen
	• rolling a number that is an integer	• certain to happen
	• rolling a negative number	• certain not to happen

Equally Likely:

When rolling a "fair" die, the probability of rolling a number 1, 2, 3, 4, 5 or 6
has the same chance of happening.
Each value is "equally likely to occur".
When probability is equally likely to occur, the situation is described as being "fair".
There are oddly shaped, or weighted, die where the faces are not equally likely to occur when tossed.
Equally likely to occur means that the possible results will occur with equal probability
(which may also be referred to as a "uniform" probability model).
One outcome is not more likely to occur than any other.

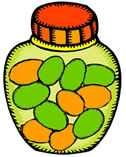
Now, consider the example of drawing a bean from a jar containing 6 green beans and 5 orange beans. Since there are more green beans than orange beans, there is a greater possibility of drawing a green bean. When drawing a bean, the color choices are not equally likely to occur (not uniform probability). The probability of drawing a green bean is 6/11. The probability of drawing an orange bean is 5/11.

Notations:

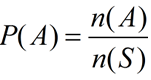• n(A) is the "number of " outcomes occurring for event A. • n(S) is the "number of " outcomes for sample space S. • The probability of event A is represented as P(A)