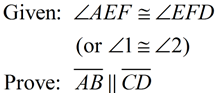|
On the page Angles and Parallel Lines, we saw four major angles associated directly
with parallel lines and the theorems describing the angles status given the lines to be parallel.
Also, on that page, we saw the "converse" of those theorems.
These "converse" theorems establish our toolbox for proving lines to be parallel.
On the page Verifying Angle Theorems for Parallel Lines, we saw the proofs of the status of the angles given that the lines were parallel. On this page, we will use the status of those angles to "prove" that the lines are parallel.
We will prove geometrically that these "converse" theorems are true,
and establish these theorems as a popular means of proving lines parallel.
Note: The proofs shown on this page do not rely on any of the original angle theorems, or their converses theorems, as reasons for proving any of the Converse Theorems to be true.

 "Prove" Parallel Lines, given angles congruent (or supplementary) "Prove" Parallel Lines, given angles congruent (or supplementary)

In "Method 1", we will show that all four converse theorems can be proven true.
All four angle types will be discussed in connection to one basic proof to prove lines parallel starting with congruent alternate interior angles.
We will be using the first completed proof as a template,
and indicating only a few adjustments to address additional angles.
Method 1: (Two Column Proof)
Alternate Interior Angles
 Converse
Converse |
If two lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel. |
|
 |
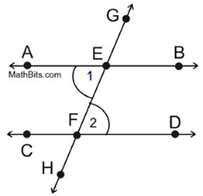
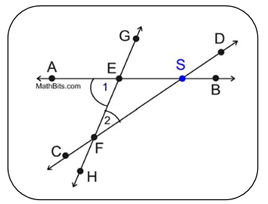
Given: lines m, p both cut by transversal t
at point B, A respectively.
 and and 
Prove: m || p
|
The idea behind this proof is to utilize congruent triangles.
An auxiliary line will be drawn to form the triangles.
This proof is based upon starting with the "acute" alternate interior angles,  . .
If you wish to start with the "obtuse" alternate interior angles,  , simply establish their connection to angles 1 and 2 (inside the triangles), then proceed with this same proof. , simply establish their connection to angles 1 and 2 (inside the triangles), then proceed with this same proof.
Supply before Step 1:
• ∠3 supp ∠1, ∠4 supp ∠2 - linear pairs form supp. angles
•
 - supplements of congruent angles are congruent. - supplements of congruent angles are congruent.

Let's connect alternate exterior, corresponding, and interior angles on
the same side of the transversal to the proof shown above.
Alternate Exterior Angles:
 Converse
Converse |
If two lines are cut by a transversal and the alternate exterior angles are congruent, the lines are parallel. |
|
To show that congruent exterior angles will also prove the lines parallel, we will establish a connection between the exterior angles and angles 1 and 2, which are inside the triangles. We can then proceed with the prove shown above.
Given: 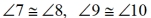
Corresponding Angles:
 Converse
Converse |
If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel. |
|
In a similar manner, we will establish a connection between the congruent corresponding angles
and angles 1 and 2, inside the triangles. This will allow us to proceed with the proof
shown above.
Given: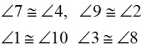
Interior Angles on the Same Side of the Transversal:
 Converse
Converse |
If two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, the lines are parallel. |
|
Yet again, we will establish a connection between the interior angles on the same side of the transversal and angles 1 and 2 inside the triangles. This will allow us to proceed with the proof shown above to finish the proof.
Given: ∠1 supp ∠4; ∠ 3 supp ∠ 2
 |
Additional starting statements & reasons:
• m∠1 + m ∠4 = 180; m∠2 + m ∠3 = 180
- supp ∠s are 2 ∠s adding to 180
•∠2 supp ∠4; ∠1 supp ∠3
- linear pairs form supp angles
• m∠2 + m ∠4 = 180; m∠1 + m ∠3 = 180
- supp ∠s are 2 ∠s adding to 180
• m∠1 + m ∠4 = m∠2 + m ∠4
m∠2 + m ∠3 = m∠1 + m ∠3 - substitution
• m∠1 = m∠2
- subtraction postulate of equality
•  - congruent ∠s have = measure. - congruent ∠s have = measure.
|
| Now, pick up with Step 2 of the proof shown above to complete the proof. |


In "Method 2", we will be dealing only with a proof regarding alternate interior angles.
This proof is an indirect proof, so a different style of reasoning is being used.
 Converse
Converse |
If two lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel. |
|
Method 2: (Indirect Proof)
 |
1. 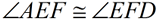 (or ∠1 (or ∠1 ∠2} ∠2} |
1. Given |
|
2. Assumption leading to a contradiction. |
|
3. In a plane, two distinct lines are either parallel or intersecting. |
4. 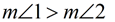 |
4. The measure of an exterior angle of a triangle is greater than the measure of either non-adjacent interior angle. |
5. 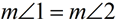 |
5. Congruent angles are angles of equal measure. |
|
6. Contradiction steps 4 and 5.
|
|
Remember: By the Law of Trichotomy, only one of these statements can be true.
m∠1 = m∠2, or m∠1 < m∠2,
or m∠1 > m∠2.
"equal to" or "less than" or "greater than"
"for two real numbers a and b, a is either equal to b, greater than b, or less than b."

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|