This page will take a look at a few of the various examples that utilize the concept of slopes associated with parallel and perpendicular lines.
 Questions Asking Directly for Equations of Parallel or Perpendicular Lines: Questions Asking Directly for Equations of Parallel or Perpendicular Lines: |
| 1. What is the equation of a line parallel to y = -4x + 5 and passing through the point (6,-3)? |
Solution: The slope of the given line, y = -4x + 5 is -4 (remember y = mx + b).
Since parallel lines have = slopes, our line has a slope of -4.
Use the point -slope form of the equation of a line: y - y1 = m(x - x1).
m = -4 (x1, y1) = (6,-3)
ANSWER: y - (-3) = -4(x - 6)
y + 3 = -4x + 24
y = -4x + 21
| 2. What is the equation of a line perpendicular to 2y = x - 4 and passing through the point (-4,1)? |
Solution: The slope of the given line, 2y = x - 4 is ½ (remember to solve for y first).
Since perpendicular lines have negative reciprocal slopes, our line has a slope of -2.
Use the point-slope form of the equation of a line: y - y1 = m(x - x1).
m = -2 (x1, y1) = (-4,1)
ANSWER: y - 1 = -2(x - (-4))
y -1 = -2x - 8
y = -2x - 7
 Questions Asking Indirectly for Equations of Perpendicular Lines: Questions Asking Indirectly for Equations of Perpendicular Lines: |
| 3. What is the equation of a line tangent to a circle whose equation is
(x - 5)2 + (y + 2)2 = 25 at the point (8,-4), which lies on the circle ? |
Solution: The circle (x - 5)2 + (y + 2)2 = 25 has a center at (5,-2) and a radius of 5.
A tangent to a circle is perpendicular to the radius at the point of tangency.
Find the slope of the radius: 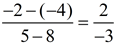
The slope of the tangent will be 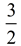 .
.
ANSWER: 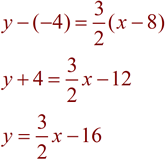
| 4. A line through point (-3,4) is perpendicular to the line y = 2x - 3. Find the point where the lines intersect. |
Solution: If we know the equation of the perpendicular line, we will be able to set up a system of equations to find the point of intersection. The slope of the perpendicular line is the negative reciprocal of 2, or -½.
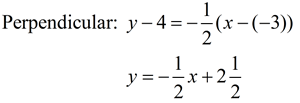
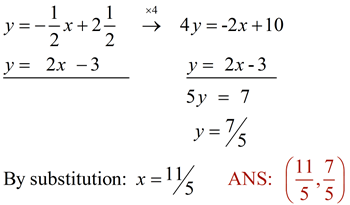
|
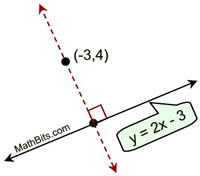
Do not make the assumption that your answer (the ordered pair) will be integer values. |
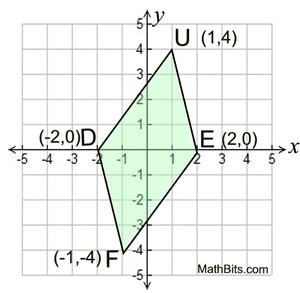
| 5. Find the area of parallelogram DUEF, as shown below, by finding its base and a height to that base. (Round area to nearest square unit). |
Solution: This problem is stating a "specific" way you must find the area. The difficulty is that we cannot "count" either the base or the height in this problem. We can find a base length using the distance formula, but the height will require more work.
We will use base length FE.
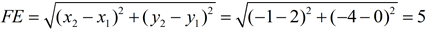
A height to this base can be drawn from point D. But we need to know the point where the height will hit the base. This will be accomplished just as it was in example 4.
First the equation of the line through F and E:
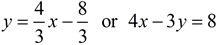
|
|
The perpendicular height will have a slope of -3/4 and pass through D(-2,0).
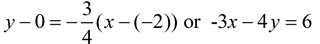
Now, find the intersection point:
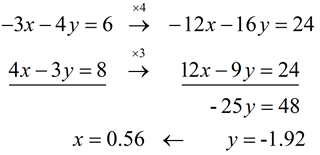
Find the length of the height from D(-2,0) to (0.56,-1.92).
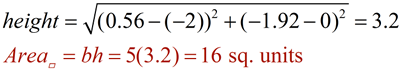
|