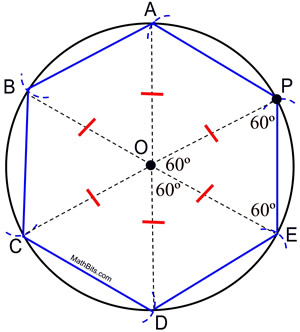
STEPS: 2. Place a dot, labeled P, anywhere on the circumference of the circle to act as a starting point. 3. Without changing the span on the compass, place the compass point on P and swing a small arc crossing the circumference of the circle. 4. Without changing the span on the compass, move the compass point to the intersection of the previous arc and the circumference and make another small arc on the circumference of the circle. 5. Keep repeating this process of "stepping" around the circle until you return to point P. 6. Starting at P, connect to each arc on the circle forming the regular hexagon.
Proof of Construction: PA = AB = BC = CD = DE since these lengths represent copies of the radius of circle O. But how do we know for sure that the last length, EP, coincided exactly with point P? Is EP actually the same length as the other copied radii? ΔDOE is an equilateral triangle since it has 3 sides of equal length (DO and OE are radii lengths and DE is a copy of this radii length). In the same manner, ΔCOD, ΔBOC. ΔAOB and ΔPOA are also equilateral triangles. Since the interior angles of an equilateral triangle each contain 60º, m∠COD = m∠BOC = m∠AOB = m∠POA = m∠DOE = 60º. Since all of the central angles (surrounding a point) must add to 360º, we know the m∠POE = 60º (360º - 300º = 60º). Since
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|